Коронная передача: 8.2: Передача механической мощности – Планетарная передача — Википедия

8.2: Передача механической мощности

Как описывалось в Блоке 7, мощность представляет собой коэффициент проделанной работы (например, насколько быстро ученик может нести рюкзак, нагруженный книгами весом 15 фунтов, вверх по лестнице). Мощность также может пониматься как коэффициент преобразования энергии (например, насколько быстро ученик может преобразовать химическую энергию мышц в механическую энергию для подъема рюкзака вверх по лестнице).

Передача мощности определяется как передача энергии из источника ее генерирования или хранения в точку ее рабочего применения. Посмотрите на электричество: электрическая энергия хранится в батарее, затем передается по проводам к электромотору, где преобразуется в механическую энергию работы.

Механическая мощность может быть передана на большие расстояния различными способами. В данном блоке основной акцент будет сделан на передачу механической энергии в форме вращательного движения (например, если присутствует ввод от стороны вращения при определенном крутящем моменте, мощность которого необходимо преобразовать в другую форму на выходе).

Ось передает движение от точки к точке по оси движения. Одним из распространенных примеров этого процесса является ведущая ось автомобиля. В осях мощность передается через шпонки, шлицы и многоугольные оси.

В VEX в качестве элемента системы движения используются четырехсторонние многоугольные (квадратные) оси. Это означает, что ось будет передавать крутящий момент непосредственно к любому элементу с квадратным отверстием, соответствующем форме оси. Квадратная ось имеет скругленные грани, что позволяет использовать ее также в конструкциях с круглыми отверстиями. 

Еще одним способом передачи механической мощности являются зубчатые передачи (ЗП). Существует множество различных зубчатых передач, часто встречающихся в мире.

ЦИЛИНДРИЧЕСКИЕ ПРЯМОЗУБЫЕ ПЕРЕДАЧИ:

Наиболее распространенным типом передач являются цилиндрические прямозубые передачи. Когда люди думают о передачах, они представляют именно их.

Цилиндрические прямозубые шестерни передают движение между двумя валами, вращающимися параллельно друг другу. Эти шестерни характеризуются формой зубьев, расположенных прямо и параллельно оси, на которой вращаются. Эти основная форма передачи механической мощности в системе проектирования VEX Robotics Design System. Помимо прочего, цилиндрические прямозубые передачи встречаются практически во всех существующих в мире механизмах, от автомобилей до механизмов, открывающих лотки DVD-плееров.

КОНИЧЕСКИЕ ЗУБЧАТЫЕ ПЕРЕДАЧИ:

Конические шестерни имеют форму конуса и передают мощность между валами, оси движения которых пересекаются.

  

Конические передачи могут передавать мощность между валами при разных углах, но наиболее распространенным типом конической передачи является передача с углом 90 градусов, как показано в примере выше.

КОРОННЫЕ ЗУБЧАТЫЕ ПЕРЕДАЧИ:

Коронные шестерни представляют собой разновидность конических шестерен, где зубья располагаются перпендикулярно торцу шестерни.

Коронные шестерни могут зацепляться с коническими и цилиндрическими прямозубыми шестернями (как показано в примере выше) таким образом, чтобы движение передавалось между валами с пересекающимися осями вращения.. 

ЧЕРВЯЧНЫЕ ЗУБЧАТЫЕ ПЕРЕДАЧИ:

Червячные передачи всегда состоят из червячной шестерни (червяка) и червячного колеса, зацепляющихся друг с другом для передачи мощности между перпендикулярными валами, оси вращения которых располагаются на удалении друг от друга.

.

Червячная шестерня по форме напоминает винт. При вращении она поворачивается, зацепляясь с червячным колесом. Данный тип парной передачи используется для создания большого механического преимущества в пределах малого пространства. В этой парной передаче, червячная шестерня может направлять червячное колесо, но червячное колесо не может управлять движением червячной шестерни. Поэтому червячные передачи полезны в механизмах, где необходимо исключить возможность обратного хода.

КОСОЗУБЫЕ ЦИЛИНДРИЧЕСКИЕ ПЕРЕДАЧИ:

Косозубые шестерни напоминают по форме цилиндрические, но их зубья закручены по форме спирали. Эти шестерни могут использоваться для передачи мощности между двумя параллельными либо между двумя перпендикулярными не пересекающимися осями движения.

ЭПИЦИКЛИЧСКИЕ (ПЛАНЕТАРНЫЕ) ЗУБЧАТЫЕ ПЕРЕДАЧИ:

Комплект эпициклических, или планетарных, шестерен состоит из одной или нескольких планетарных шестерен (Planet), вращающихся по шестерне внешнего кольца и приводимых в движение центральной шестерней (Sun). Перемещаясь, планетарные шестерни обычно одновременно двигают водило планетарной передачи.

Интересно то, что планетарные передачи могут использоваться несколькими способами, при этом разные шестерни будут выполнять функции входов и выходов. Например, центральная шестерня (Солнце) может использоваться в качестве входа, а водило — в качестве выхода, если кольцевая шестерня находится в неподвижном положении, либо кольцевая шестерня может использоваться в качестве входа и центральная — в качестве выхода, если водило находится в неподвижном положении. Суммарное механическое преимущество планетарной передачи изменяется в зависимости от используемой конфигурации.

РЕЕЧНЫЕ ПЕРЕДАЧИ:

Реечная передача — это передача, монтируемая на прямой рейке таким образом, чтобы при приложении крутящего момента со стороны цилиндрической шестерни (шестерни зубчатой рейки) она перемещалась линейно.

Реечные передачи часто используются для преобразования вращательного движения в линейное движение. В автомобилях данный тип передач используется для преобразования вращательного движения рулевого колеса в линейное движение влево и вправо для управления направлением движения автомобиля. Поэтому тип управления автомобилем называется «реечным».

В соревновательной робототехнике существует множество применений реечной шестерни для создания линейных исполнительных механизмов для приводов.

Планетарная передача — Википедия

Планетарная передача с остановленным водилом по сути является двухступенчатой зубчатой передачей с неподвижными осями колес. Планетарная передача (солнечная шестерня остановлена) Планетарная передача (коронная шестерня остановлена) Схема эпициклически движущейся планеты

Планетарная передача (далее — ПП) — механическая передача вращательного движения, за счёт своей конструкции способная в пределах одной геометрической оси вращения изменять, складывать и раскладывать подводимые угловые скорости и/или крутящий момент. Обычно является элементом трансмиссии различных технологических и транспортных машин.

Конструктивно ПП всегда представляет собой набор взаимозацепленных зубчатых колёс (не менее 4), часть из которых (не менее 2) имеет общую геометрическую неподвижную ось вращения, а другая часть (также, не менее 2) имеет подвижные оси вращения, концентрически вращающиеся на так называемом «водиле» вокруг неподвижной. Зубчатые колёса на неподвижной оси всегда связаны друг с другом не напрямую, а через зубчатые колёса на подвижных осях, а ввиду того, что вторые способны не только вращаться относительно первых, но и обкатывать их, тем самым передавая поступательное движение на водило, все звенья ПП, на которые можно подавать/снимать мощность, получают возможность вращаться дифференциально, с тем лишь условием, что угловая скорость любого такого звена не абсолютно хаотична, а определяется угловыми скоростями всех остальных звеньев. В этом плане ПП похожа на планетарную систему, в которой скорость каждой планеты определяется скоростями всех остальных планет системы. Дифференциальный принцип вращения всей системы, а также то, что в своём каноническом виде набор зубчатых колёс, составляющих ПП, собран в некоем подобии солнца и эпициклически движущихся по орбите планет, даёт данной механической передаче такие присущие только ей интернациональные определения, как

планетарная, дифференциальная (от лат. differentia — разность, различие) или эпициклическая, каждое из которых в данном случае есть синонимы.

С точки зрения теоретической механики планетарная передача — это механическая система с двумя и более степенями свободы. Эта особенность, являющаяся прямым следствием конструкции, есть важное отличие ПП от каких-либо других передач вращательного движения, всегда имеющих только одну степень свободы. И эта особенность наделяет саму ПП тем важным качеством, что в аспекте воздействия на угловые скорости вращения ПП может не только редуцировать эти скорости, но и складывать и раскладывать их, что, в свою очередь, делает её основным механическим исполнительным узлом не только различных планетарных редукторов, но таких устройств, как дифференциалы и суммирующие ПП.

Планетарная передача и планетарный механизм[править | править код]

В русскоязычной инженерной терминологии термины планетарная передача (далее — ПП) и планетарный механизм (далее — ПМ) зачастую предполагаются как синонимы. Отличия в том, что термин ПП обычно используется в контексте принципиального понимания устройства той или иной передачи вращательного движения, особенно если устройство такой передачи не очевидно (скрыто корпусом/картером) или такая передача обладает определёнными уникальными свойствами, присущими только планетарной, и на этом надо акцентировать внимание. А термин ПМ используется для обозначения конкретного зубчато-рычажного механизма, причём существуют критерии, позволяющие чётко описать ПМ как сборочный узел в составе более крупного узла или агрегата и определить, сколько и каких именно использовано ПМ в конкретной передаче вращательного движения.

Состав планетарного механизма[править | править код]

Конструкция ПП/ПМ основана на различных комбинациях из трёх основных и нескольких одинаковых вспомогательных звеньев. Три основные звена с одной общей осью вращения — два центральных зубчатых колеса и водило. Вспомогательные звенья — набор одинаковых зубчатых колёс на подвижных осях вращения и подшипники.

• Малое центральное зубчатое колесо с внешними зубьями называется солнечной шестернёй или солнцем (С).
• Большое центральное зубчатое колесо с внутренними зубьями называется коронной, эпициклической шестернёй или эпициклом (Э).
• Водило (В) является основой ПМ — это неотъемлемая деталь абсолютно любого ПМ и краеугольный камень всей идеи передачи вращения через планетарную систему с дифференциальной связью. Водило представляет собой рычажный механизм — обычно такую пространственную вилку, ось «основания» которой совпадает с осью самого ПМ, а оси «зубцов» с установленными на них сателлитами концентрически вращаются вокруг неё в плоскости/плоскостях расположения центральных зубчатых колёс. Оси «зубцов» — это и есть так называемые подвижные оси или оси сателлитов
• Сателлиты () представляют собой зубчатые колёса (или группы колёс) с внешними зубьями. При этом сателлиты находятся в одновременном и постоянном зацеплении с обоими центральными зубчатыми колёсами ПМ. Количество сателлитов в ПМ обычно составляет от двух до шести (чаще всего — три, так как только при трёх сателлитах нет нужды в специальных уравновешивающих механизмах) и точного значения для функциональности ПМ не имеет. В различных ПМ применяются сателлиты одновенцовые (одно простое зубчатое колесо), двухвенцовые (два соосных зубчатых колеса с общей ступицей), трёхвенцовые и так далее. Также сателлиты могут быть парными — то есть, располагающимимся на осях одного водила и зацепленными в паре.

Зубчатые колёса, составляющие ПМ, могут быть любого известного типа: прямозубые, косозубые, шевронные, червячные. Тип зацепления в общем случае не важен и на принципиальную работу ПП влияния не оказывает.

В любом ПМ оси вращения центральных зубчатых колёс и водила всегда совпадают. Однако это не значит, что оси сателлитов всегда будут параллельны основной оси. Как и в случае с простыми зубчатыми передачами, здесь возможны варианты параллельных, скрещивающихся и пересекающихся осей. Пример второго варианта — межколёсный дифференциал с коническими зубчатыми колёсами. Пример третьего варианта — самоблокирующийся дифференциал Torsen с червячным зацеплением.

Любой ПМ, независимо простой он или сложный, плоский или пространственный, для своей работоспособности должен иметь одно водило с сателлитами и не менее двух любых центральных зубчатых колёс. Под определением «два любые» подразумевается, что это могут быть не только одно солнце и один эпицикл, но и два солнца и ни одного эпицикла, или два эпицикла и ни одного солнца. Три звена, в том числе водило, есть необходимое и достаточное условие для того, чтобы ПМ мог выполнять функции передачи мощности и сложения/разложения потоков: работать в качестве редуктора (в том числе многоскоростного), в качестве дифференциала или суммирующей ПП. Также три звена есть основа такого русскоязычного технического термина, как Трёхзвенный Дифференциальный Механизм (или ТДМ).

Формально, механизмы, состоящие всего из двух звеньев — из водила и всего лишь одного центрального зубчатого колеса — также могут именоваться планетарными. Фактически же, такие двухзвенные ПМ трудно разумно приспособить для выполнения какой-либо работы: они не годятся для передачи мощности с одного основного звена на другое и лишь при определённых условиях могут работать как переусложнённая прямая передача. Увеличение числа основных звеньев одного ПМ в большую сторону — до 4 и более — возможно и формально и фактически, однако при этом такие ПМ не приобретают никаких новых свойств, хотя и получают больше теоретически доступных передаточных отношений и могут давать проектируемой ПП определённые компоновочные преимущества.

Простые и сложные ПМ, планетарный ряд[править | править код]

Схемы наиболее распространённых сложных планетарных механизмов

Критерием деления ПМ на простые и сложные является число составляющих его основных звеньев (именно основных, а число сателлитов — не в счёт). Простой ПМ имеет всего три основных звена: одно водило и два любых центральных зубчатых колеса. Кинематика допускает всего-лишь 7 (семь!) ПМ, подпадающих под это условие: один наиболее распространённый и всем известный, так называемый «элементарный», с набором одновенцовых сателлитов схемы ; три ПМ с двухвенцовыми саттелитами (, , ) и три ПМ с парными взаимозацепленными сателлитами (СВЭ, СВС, ЭВЭ)).

Сложных ПМ гораздо больше чем простых. Их точное число не определено ввиду отсутствия такой нужды, а наиболее распространённые из них приведены на рисунке. Точно так же как и простые ПМ, сложные имеют всего одно водило, но центральных зубчатых колёс может быть три и более. При этом в составе сложного ПМ всегда умозрительно можно выделить несколько простых ПМ (конкретно: три в четырёхзвенном и шесть в пятизвенном), каждый из которых в себя включает два каких-то центральных зубчатых колеса и одно общее водило.

Каждый набор из центральных зубчатых колёс и сателлитов, вращающихся в одной плоскости, образует так называемый планетарный ряд. Простой ПМ с набором одновенцовых сателлитов является однорядным. Все три простые ПМ с двухвенцовыми сателлитами — двухрядные. ПМ с парными взаимозацепленными сателлитами схемы СВЭ — однорядный; схем СВС и ЭВЭ — двухрядные. Таким образом, все простые ПМ могут быть или однорядными или двухрядными. Сложные ПМ, в свою очередь, могут быть двух, трёх и четырёхрядные. Верхнее число рядов в сложном ПМ формально не ограничено, хотя фактически уже пятирядные есть большая редкость, хотя в сборках из планетарных механизмов, применяющихся в многоступенчатых планетарных коробках передач, общее число рядов может быть пять и больше. Нередко термины ПМ и планетарный ряд предполагаются как синонимы, но, в общем случае, это неверно: даже если в отдельных случаях оба термина могут обозначать одно и то же, всегда следует помнить, что их смыл несколько разный.

Плоские и пространственные ПМ[править | править код]

Свободный дифференциал на основе простого плоского двухрядного ПМ с парными сателлитами Свободный дифференциал на основе пространственного ПМ с коническими шестернями

Наличие в составе одного ПМ более одного планетарного ряда не означает, что он является пространственным. Сколько бы ни было рядов, но если плоскости вращения всех составляющих каждый ряд зубчатых колёс параллельны, то такой ПМ будет оставаться плоским. Критерием отличия плоского ПМ от пространственного является наличие не просто более одной плоскости вращения составляющих его зубчатых колёс, но наличие непараллельных плоскостей их вращения. Плоскости вращения звеньев в пространственном ПМ не обязаны быть строго перпендикулярны друг-другу и могут находиться под любыми произвольными углами. Примером пространственного ПМ может служить конический симметричный дифференциал, наподобие применяющегося в приводе ведущих колёс автомобиля. А вот близкий по конструкции цилиндрический дифференциал, применяющийся там же и выполняющий точно такие же функции, будет оставаться плоским ПМ.

Пространственные ПМ по своему функционалу ничем не отличаются от аналогичных по составу плоских ПМ. Выбор того или иного ПМ в качестве основы конкретной ПП есть лишь вопрос экономики или конструкторских предпочтений. Тот же простой межколёсный дифференциал почти всегда выполнен на основе пространственного ПМ не потому, что что плоский не годится, а, скорее, по определённым компоновочным соображениям. Плюс, как это ни странно, пространственный ПМ для выполнения схожих функций может требовать меньшего количества шестерён и деталей вообще. Так, тот же межколёсный дифференциал в пространственном варианте требует всего лишь 4 одинаковые шестерни, из которых две пойдут на два солнца и две — на два саттелита. В случае же плоского варианта, таких шестерён потребуется как минимум шесть, а скорее всего — восемь, и при этом они обязательно будут двух разных типоразмеров.

2 степени свободы ПМ[править | править код]

Уникальной особенностью любого ПМ, отличающей его от всех прочих зубчатых передач, является наличие у него двух степеней свободы. Применительно к простому трёхзвенному ПМ это означает, что понимание угловой скорости вращения любого одного основного звена не даёт однозначного понимания угловых скоростей двух других основных звеньев, даже если известны все передаточные отношения внутри ПМ. Здесь все три основных звена находятся в дифференциальной связи друг с другом и для определения их угловых скоростей надо знать угловые скорости как минимум двух из них. В этом есть важное отличие ПМ от прочих зубчатых механизмов, в которых угловые скорости всех элементов связаны линейной зависимостью, а по угловой скорости одного элемента всегда можно точно определить угловые скорости всех остальных элементов, сколь много их бы не было. И в этом есть основа уникальных свойств, присущих любому ПМ: способность изменять угловые скорости на выходе при неизменных угловых скоростях на входе, способность делить и суммировать потоки мощности и всё это при постоянно зацепленных шестернях.

Любой ПМ, независимо от того, простой он или сложный, имеет фактически лишь две степени свободы. Для простого ПМ это подтверждается и визуальным наблюдением за работой такого механизма и уравнением Чёбышева. Для сложных ПМ это визуально не очевидно, а уравнение Чёбышева теоретически может допускать существование для таких ПМ трёх степеней свобод, что подразумевает наличие четырёх звеньев, находящихся в дифференциальной связи друг с другом. Но фактически такие сложные ПМ будут физически неработоспособны в тех практических задачах, ради которых они создаются, а все работоспособные сложные ПМ останутся двухстепенными. Независимо от числа основных звеньев любого работоспособного сложного ПМ, в нём, так же как и в простом ПМ, в дифференциальной связи друг с другом будет находиться только три основных звена, а остальные основные звенья, сколько бы их ни было, будут иметь линейную связь с каким-то одним из трёх вышеупомянутых. Попытки же создания сложных ПМ с тремя (и тем более, с четырьмя) фактическими степенями свободы считаются бесперспективными, а все работоспособные трёх- и четырёхстепенные ПП основаны на сборке последовательно взаимозацепленных двухстепенных ПМ.

Передаточное отношение[править | править код]

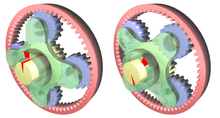Планетарная передача в режиме повышения скорости. Водило (зелёное) вращается внешним источником. Усилие снимается с солнечной шестерни (жёлтая), в то время как кольцевая шестерня (красная) закреплена неподвижно. Красные метки показывают вращение входного вала на 45°.

Передаточное отношение такой передачи визуально определить достаточно сложно, в основном, потому что система может приводиться во вращение различными способами.

При использовании планетарной передачи в качестве редуктора один из трёх её основных элементов фиксируется неподвижно, а два других служат в качестве ведущего и ведомого. Таким образом, передаточное отношение будет зависеть от количества зубьев каждого компонента, а также от того, какой элемент закреплён.

Рассмотрим случай, когда водило зафиксировано, а мощность подводится через солнечную шестерню. В этом случае планетарные шестерни вращаются на месте со скоростью, определяемой отношением числа их зубьев относительно солнечной шестерни. Например, если мы обозначим число зубьев солнечной шестерни как S{\displaystyle S}, а для планетарных шестерён примем это число как P{\displaystyle P}, то передаточное отношение будет определяться формулой SP{\displaystyle {\frac {S}{P}}}, то есть если у солнечной шестерни 24 зуба, а у планетарных по 16, то передаточное отношение будет −2416{\displaystyle -{\frac {24}{16}}}, или −32{\displaystyle -{\frac {3}{2}}}, что означает поворот планетарных шестерён на 1,5 оборота в противоположном направлении относительно солнечной.

Далее вращение планетарных шестерён может передаваться кольцевой шестерне, с соответствующим передаточным числом. Если кольцевая шестерня имеет A{\displaystyle A} зубьев, то оно будет вращаться с соотношением PA{\displaystyle {\frac {P}{A}}} относительно планетарных шестерён. (В данном случае перед дробью нет минуса, так как при внутреннем зацеплении шестерни вращаются в одну сторону). Например, если на кольцевой шестерне 64 зуба, то относительно приведённого выше примера это отношение будет равно 1664{\displaystyle {\frac {16}{64}}}, или 14{\displaystyle {\frac {1}{4}}}. Таким образом, объединив оба примера, мы получим следующее:

• Один оборот солнечной шестерни даёт −SP{\displaystyle -{\frac {S}{P}}} оборотов планетарных шестерён;
• Один оборот планетарной шестерни даёт PA{\displaystyle {\frac {P}{A}}} оборотов кольцевой.

В итоге, если водило заблокировано, общее передаточное отношение системы будет равно −SA{\displaystyle -{\frac {S}{A}}}.

В случае, если закреплена кольцевая шестерня, а мощность подводится к водилу, передаточное отношение на солнечную шестерню будет меньше единицы и составит 1(1+AS){\displaystyle {\frac {1}{(1+{\frac {A}{S}})}}}.

Если закрепить кольцевую шестерню, а мощность подводить к солнечной шестерне, то мощность должна сниматься с водила. В этом случае передаточное отношение будет равно 1+AS{\displaystyle 1+{\frac {A}{S}}}. Это самое большое передаточное число, которое может быть получено в планетарной передаче. Такие передачи используются, например, в тракторах и строительной технике, где требуется большой крутящий момент на колёсах при невысокой скорости.

Всё вышесказанное можно описать следующими двумя уравнениями (выведены из условия отсутствия проскальзывания сопрягаемых шестерён и следовательно равенства дуг, проходимых точками, находящихся на окружностях, в единицу времени):

A(ωa−ωc)=PωpS(ωs−ωc)=−Pωp{\displaystyle {\begin{aligned}A\left(\omega _{a}-\omega _{c}\right)=P\omega _{p}\\S\left(\omega _{s}-\omega _{c}\right)=-P\omega _{p}\end{aligned}}}

Здесь ωa,ωc,ωp,ωs{\displaystyle \omega _{a},\omega _{c},\omega _{p},\omega _{s}} — угловые скорости соответственно: кольцевой шестерни, водила, планетарных шестерён относительно водила, и солнечной шестерни. Первое уравнение характеризует вращение водила относительно кольцевой шестерни, второе — солнечной шестерни относительно водила.

Если исключить из уравнений ωp{\displaystyle \omega _{p}} путём их сложения — получится одно уравнение: Aωa+Sωs=(A+S)ωc{\displaystyle A\omega _{a}+S\omega _{s}=(A+S)\omega _{c}}. Так как числа зубьев шестерён всегда удовлетворяют условию A=S+2P{\displaystyle A=S+2P} (исходя из простых геометрических соотношений, поскольку в диаметр коронной шестерни помещается диаметр солнечной шестерни и два диаметра сателлитов), по-другому это уравнение можно записать как:

(2+n)ωa+nωs−2(1+n)ωc=0{\displaystyle \left(2+n\right)\omega _{a}+n\omega _{s}-2\left(1+n\right)\omega _{c}=0}

Где n — это параметр передачи, равный n=SP{\displaystyle n={S \over P}}, то есть отношению чисел зубьев солнечной и планетарных шестерён.

В нижеуказанной таблице (указывающей выходные скорости различных типов планетарных передач в зависимости от их конструктивных особенностей) приняты следующие условные обозначения:

Планетарный редуктор — Википедия

Планетарный редуктор.
Опорное звено эпицикл заблокировано на корпус редуктора.

Планета́рный реду́ктор, дифференциа́льный реду́ктор (от лат. differentia – разность, различие) — один из классов механических редукторов. Редуктор называется планетарным из-за планетарной передачи, находящейся в редукторе, передающей и преобразующей крутящий момент.

Колёсный редуктор военного автомобиля МАЗ-7310. Водило с сателлитами сняты

Конструкция[править | править код]

Механической основой планетарного редуктора может быть планетарная передача любой формы и состава. Принципиальная возможность работы планетарной передачи в режиме редуктора не зависит от формата распределения функций между тремя её основными звеньями (солнечной шестернёй, водилом с шестернями сателлитами и коронной шестернёй): любое звено может быть выбрано конструкторами как ведущее, и любое как ведомое. Но при этом, наличие у планетарной передачи двух степеней свобод требует снятия одной степени свободы для её работы в качестве редуктора; эта задача решается посредством блокировки третьего звена на корпус редуктора, а само звено получает название «опорное звено».

Уникальные особенности[править | править код]

В контексте сравнения планетарной передачи с любыми другими типами зубчатых передач под использование их в качестве редуктора, таковыми особенностями являются: соосность входящего и исходящего потока мощности (например, валов) даже на однорядной планетарной передаче; возможность выбора из шести передаточных отношений даже на простой трёхзвенной планетарной передаче; две степени свободы любой планетарной передачи; возможность получения больших передаточных отношений в условиях ограниченного поперечного габарита.

Типы планетарных редукторов и их применение[править | править код]

Планетарный редуктор с одной степенью свободы[править | править код]

В таких редукторах опорное звено всегда заблокировано на корпус редуктора. При этом для любой трёхзвенной планетарной передачи возможны шесть вариантов распределения ролей между тремя основными звеньями, что даёт шесть передаточных отношений, три из которых могут применяться для редукторов (передаточное отношение больше единицы) и три для мультипликаторов (передаточное отношение меньше единицы).

Наиболее глубокую редукцию в схеме СВЭ даёт вариант 1 (с солнечной шестерни на водило), наиболее слабую — вариант 3 (с коронной шестерни на водило). Некое промежуточное значение редукции с обязательным противовращением даёт Вариант 5 (с солнечной шестерни на коронную), но в силу разных причин его используют не часто (единственный известный пример — колёсные редукторы дорожных автомобилей МАЗ). Оставшиеся три варианта дают мультипликацию, в том числе одно передаточное отношение обратного вращения.

Планетарные редукторы с одной степенью свободы применяются в бортовых главных передачах гусеничных машин, в двухступенчатых главных передачах колёсных грузовых машин в ступицах ведущих колёс, в грузовых лебёдках и тельферах, в автомобильных стартёрах, в совмещённых планетарных мотор-редукторах. Общий принцип применения — требование компактности редуктора и соосности ведущего и ведомого валов. В грузовых лебёдках и тельферах могут применяться двух- и трёхрядные планетарные передачи, а общее передаточное отношение таких планетарных редукторов может быть порядка 100.

Планетарный редуктор с двумя степенями свободы[править | править код]

Конструктивно подобный планетарный редуктор может быть аналогичен планетарному редуктору с одной степенью свободы, с тем лишь отличием, что опорное звено здесь может быть разблокировано. При этом планетарная передача перестаёт выполнять редукцию и становится дифференциалом, а ввиду того, что в любом дифференциале мощность на ведомых звеньях выравнивается до минимально востребованной на любом из двух этих звеньев, настоящее ведомое звено перестаёт передавать сколь-либо существенную мощность по кинематической цепи трансмиссии и останавливается, а вращается только разблокированное опорное звено. К подобным редукторам относится термин «дифференциальный редуктор».

Применяются в однорадиусных механизмах поворота гусеничных машин, где они одновременно выполняют функцию редукции и обеспечивают возможность плавного разрыва потока мощности. Также могут применяться везде, где требуется опция отключения потока мощности без необходимости остановки мотора или вала привода ведущего звена.

Многоскоростной планетарный редуктор[править | править код]

Многоскоростные планетарные редукторы допускают переключение между различными кинематическими цепями внутри себя, то есть, дают возможность использования разных передаточных отношений. Конструктивно это всегда реализуется через применение так называемых управляющих элементов: тормозов, блокировочных фрикционов, обгонных муфт. Наличие шести передаточных отношений даже на одном простом планетарном механизме теоретически допускает его использование в качестве минимально возможного, но фактически все многоскоростные планетарные редукторы выполнены либо на основе одного сложного планетарного механизма, либо на основе нескольких последовательно зацепленных простых (и сложных) планетарных механизмов. Число степеней свободы таких редукторов может быть 2 и более, общее число управляющих элементов может быть более десяти. Все многоскоростные планетарные редукторы имеют ту особенность, что взаимная блокировка их звеньев превращает их в прямую передачу, что может быть также использовано для расширения числа доступных скоростей.

В основном применяются в трансмиссиях транспортных машин: в двухрадиусных механизмах поворота гусеничных машин, в коробках передач и раздаточных коробках колёсных и гусеничных машин, где могут выполнять как функции делителя, овердрайва, ходоуменьшителя, так и функции основного набора передач включая реверс, независимо от общего числа скоростей. Также применяются в электроинструментах, где требуется возможность получения более одной скорости вращения.

Шарикоподшипниковый редуктор[править | править код]

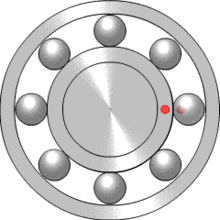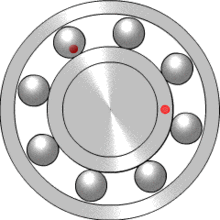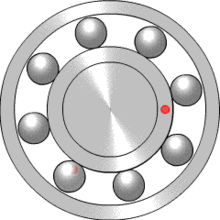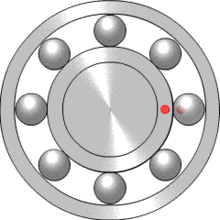
Шарикоподшипник представляет пример планетарного редуктора, в котором водилом является сепаратор, функции солнечной шестерни выполняет внутреннее кольцо, функции коронной шестерни — наружное кольцо, а сателлиты — это шарики. С использованием обыкновенных шарикоподшипников могут быть сконструированы маломощные редукторы (для научных или измерительных приборов). Например, шарикоподшипниковые планетарные редукторы используются в конструкции верньера, применяемого для точной настройки радиостанции на нужную частоту приема/передачи.

Учебный проект «КОРОННАЯ ПЕРЕДАЧА В КОНСТРУКТОРЕ Lego WeDo»

Коронная шестерня

Коронная шестерня – это особый тип шестерен, их зубья находятся на боковой поверхности. Такая шестерня работает, как правило, в паре с прямозубой или с барабаном (цевочное колесо), состоящим из стержней. Такая передача используется в башенных часах.

Просмотр содержимого документа
«Учебный проект «КОРОННАЯ ПЕРЕДАЧА В КОНСТРУКТОРЕ Lego WeDo»»

Министерство образования, науки и молодёжной политики Краснодарского края

Государственное бюджетное профессиональное образовательное учреждение Краснодарского края «Краснодарский педагогический колледж»

УЧЕБНЫЙ ПРОЕКТ ПО ДИСЦИПЛИНЕ

ЕН. 02 Информатика и информационно-коммуникационные технологии

в профессиональной деятельности

КОРОННАЯ ПЕРЕДАЧА В КОНСТРУКТОРЕ LEGO WeDo

Модель «Флюгер»

специальность Преподавание в начальных классах

Выполнили:

студентки 4 курса группы 4 «Бш»

школьного отделения

Белая Александра Николаевна,

Грабина Ирина Евгеньевна

Руководитель:

Меденец Н.А.

Краснодар, 2018 г.

КОРОННАЯ ПЕРЕДАЧА

Зубчатое колесо или шестерня— основная деталь зубчатой передачи в виде диска с зубьями на цилиндрической или конической поверхности, входящими в зацепление с зубьями другого зубчатого колеса. Зубчатые колёса обычно используются парами с разным числом зубьев с целью преобразования вращающего момента и числа оборотов валов на входе и выходе. Колесо, к которому вращающий момент подводится извне, называется ведущим, а колесо, с которого момент снимается — ведомым.

Коронная шестерня

Коронная шестерня – это особый тип шестерен, их зубья находятся на боковой поверхности. Такая шестерня работает, как правило, в паре с прямозубой или с барабаном (цевочное колесо), состоящим из стержней. Такая передача используется в башенных часах.

Где используются коронные шестерни?

Коронные шестерни работают в башенных часах. Основной признак коронной шестерни – расположение зубьев на торцевой поверхности. Зубчатая передача, образованная коронной шестерней и барабаном из стержней (цевочное колесо), является звеном работы часового механизма.

Флюгер

доклад по механике

Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное учреждение

Российский экономический университет им. Г.В.Плеханова

Факультет гостинично-ресторанной, туристической и спортивной индустрии

Кафедра технологии и организации предприятий питания

ДОКЛАД

по дисциплине «Механика»

На тему: Типы шестерней

Выполнила

студентка группы 721

очной формы обучения

Факультета гостинично-ресторанной, туристической и спортивной индустрии

Тярина Наталья

Руководитель:

Васичев Борис Никитович

Москва-2014

Введение 3

Типы шестерней 4

Прямозубые шестерни 4

Косозубые шестеренки 4

Шевронное колесо 5

Шестерни с внутренним зацеплением 5

Винтовые шестерни 6

Секторные шестерни 6

Шестерни с круговыми зубьями 7

Звездочка шестерня-звезда 7

Коронная шестерня 8

Где используются шестерни? 8

Список используемой литературы 10

Зубчатое колесо или шестерня— основная деталь зубчатой передачи в виде диска с зубьями на цилиндрической или конической поверхности, входящими в зацепление с зубьями другого зубчатого колеса. В машиностроении принято малое зубчатое колесо с меньшим числом зубьев называть шестернёй, а большое — колесом. Однако часто все зубчатые колёса называют шестернями. Зубчатые колёса обычно используются парами с разным числом зубьев с целью преобразования вращающего момента и числа оборотов валов на входе и выходе. Колесо, к которому вращающий момент подводится извне, называется ведущим, а колесо, с которого момент снимается — ведомым. Если диаметр ведущего колеса меньше, то вращающий момент ведомого колеса увеличивается за счёт пропорционального уменьшения скорости вращения, и наоборот. В соответствии с передаточным отношением, увеличение крутящего момента будет вызывать пропорциональное уменьшение угловой скорости вращения ведомой шестерни, а их произведение — механическая мощность — останется неизменным. Данное соотношение справедливо лишь для идеального случая, не учитывающего потери на трение и другие эффекты, характерные для реальных устройств.

Прямозубые шестерни

Прямозубые шестерни — самый применяемый тип зубчатых колёс. Зубья расположены в радиальных плоскостях, линия контакта зубьев пары зубчатых колес параллельна оси вращения, как и оси обеих зубчатых колес (шестеренок) располагаются строго параллельно.

Косозубые шестеренки

Косозубые шестерни – это модернизированная версия прямозубых шестерен. Зубья, в таком случае, расположены под углом к оси вращения. Зацепление зубьев этих шестерен происходит тише и плавнее, чем у прямозубых. Они применяются либо в малошумных механизмах, либо в тех которые требуют передачи большого крутящего момента на больших скоростях. К недостаткам этого типа шестерен можно отнести: увеличенную площадь соприкосновения зубьев, что вызывает значительное трение и нагрев деталей, а вследствие: потеря мощности и дополнительное использование смазочных материалов; так же механическая сила, направленная вдоль оси шестеренки, вынуждает применять упорные подшипники для установки вала.

Шевронное колесо

Шевронные шестерни решают проблему механической осевой силы, которая возникает в случае применения косозубых колес, так как зубья шевронных (елочных) колёс изготавливаются в виде буквы «V» (или же они образовываются стыковкой двух косозубых колёс со встречным расположением зубьев). Осевые механические силы обеих половин шевронной шестерни взаимно компенсируются, поэтому нет нет необходимости использования упорных подшипников для установки валов. Шевронная передача является самоустанавливающейся в осевом направлении, в следствии чего, в редукторах с шевронными колесами один из валов устанавливают на подшипниках с короткими цилиндрическими роликами — плавающих опорах.

Шестерни с внутренним зацеплением

Шестерни такого типа имеют зубья, нарезанные с внутренней стороны. При их использовании происходит одностороннее вращение ведущей и ведомой шестерен. В данной зубчатой передаче меньше затрат на трение, а значит выше КПД. Применяются зубчатые колеса с внутренним зацеплением в ограниченных по габаритам механизмах, в планетарных передачах, в шестеренных насосах, в приводе башни танка.

Винтовые шестерни

Шестерни имеют форму цилиндра с расположенными на нем зубьями по винтовой линии. Эти шестеренки используются на непересекающихся валах, которые располагаются перпендикулярно друг друга, угол между ними 90°.

Секторные шестерни

Секторная шестерня – это часть (сектор) шестерни любого типа, она позволяет сэкономить в габаритах полноценной шестерни, так как применяется в передачах, где не требуется вращение этого зубчатого колеса (шестеренки) на полный оборот.

Шестерни с круговыми зубьями

Шестерни этого типа имеют линию зубьев в виде окружности радиуса, за счет этого контакт в передаче происходит в одной точке на линии зацепления, которая располагается параллельно осям шестерен. Передачи с круговыми зубьями «Передача Новикова» имеет лучшие ходовые качества, чем косозубые – высокую плавность хода и бесшумность, высокую нагрузочную способность зацепления, но при одинаковых условиях их ресурс работы и КПД ниже, к прочему изготовление этих шестерен значительно сложнее. Поэтому применение таких шестеренок ограниченно.

Звездочка шестерня-звезда

Шестерня-звезда — это основная деталь цепной передачи, которая используется совместно с гибким элементом — цепью для передачи механической энергии.

Коронная шестерня

Коронная шестерня – это особый тип шестерен, их зубья находятся на боковой поверхности. Такая шестерня работает, как правило, в паре с прямозубой или с барабаном (цевочное колесо), состоящим из стержней. Такая передача используется в башенных часах.

Шестерни – это главная составляющая подавляющего большинства механизмов. Часы, токарные станки, коробки переключения передач, редукторы, насосы, тепловозы, электровозы, скребковые комбайны, подъемно-транспортные агрегаты и другие машины, механизмы, агрегаты, которые относятся практически ко всем отраслевым направлениям народного хозяйства, в частности, энергетике, машиностроению, металлургии, горно-шахтному оборудованию, подвижному составу железной дороги, буровому оборудованию нефтегазодобывающего промысла – малая часть в перечне сфер (формата) применения шестерен.

Коронные шестерни работают в башенных часах. Основной признак коронной шестерни – расположение зубьев на торцевой поверхности. Зубчатая передача, образованная коронной шестерней и барабаном из стержней (цевочное колесо), является звеном работы часового механизма.

Зубчатые рейки — элемент колеса с бесконечным радиусом делительной окружности. Особенности конструкции «превращают» окружность в прямую линию. Используют для преобразования поступательного движения во вращательное и наоборот. Зубчатая рейка – составная реечной передачи, используемой в зубчатых железных дорогах (наземные «фуникулеры» обеспечивающие перевозку пассажиров и грузов, в частности, в высокогорьях).

Шестерни с внутренним зацеплением – зубья данного вида шестерен отличаются нарезкой с внутренней стороны. При эксплуатации происходит вращение ведомой и ведущей шестерен в одностороннем направлении. Такой механизм отличается высоким КПД и минимальными затратами на трение. Сфера использования: привод башни танка, шестеренные насосы, планетарные передачи.

Секторные зубчатые колеса – это часть шестерни любого вида. Прекрасная возможность сэкономить в габаритах механизма. Там, где не требуется вращение зубчатого колеса в полный оборот при передачах, применяют секторные шестерни, так например, в плунжерах насосов, замках, маятниковых механизмах.

Винтовые зубчатые колеса отличаются цилиндрической формой и расположением зубьев по винтовой линии. Такой вид шестерен применяют на непересекающихся валах, которые перпендикулярны, в частности, на станках.

Интернет-источники:

http://shesterenka.com.ua/stati/vidy-zubchatyh-koles-shesteren.html

http://www.metaprom.ru/production/shesterni.html

http://amo1.com.ua/articles/61-vidy-shesteren

коробка, механизм, шестерня, ряд и расчет

Планетарная передача — вид зубчатой передачи, применяемой в механических и автоматических трансмиссиях. Помимо преобразования вращения «планетарка» способна суммировать и раскладывать мощности. Зная о планетарном механизме: что это такое, как работает, по каким критериям оценивают редуктор, станет понятно устройство и характеристики АКПП. В случае поломки расчёт передачи поможет выбрать надёжный и долговечный механизм.

Устройство и принцип работы

Планетарный механизм — это конструкция из зубчатых колёс, перемещающихся относительно центра. По центральной оси расположены колёса разного диаметра:

• малое солнечное с внешними зубцами;
• большое коронное или эпицикл с внутренними зубцами.

Между колёсами передвигаются сателлиты. Их вращение напоминает движение планет Солнечной системы. Оси сателлитов механические соединены на водиле, которое вращается относительно центральной оси.

Устройство простого планетарного блока:

• 1 эпицикл;
• 1 солнечное колесо;
• 1 водило.

Планетарный механизм собирают в каскады из двух и более звеньев на одном валу для получения широкого диапазона передач. Главной кинематической характеристикой зубчатой передачи является передаточное отношение.

Принцип работы планетарной коробки заключается в блокировке одного из основных элементов и передаче вращения через ведущее колесо. Для остановки элемента применяют тормозные ленты, блокировочные муфты, конические шестерни. Передаточное отношение меняется в зависимости от схемы закрепления. Описать принцип действия планетарного механизма удобнее на примере:

1. Корона блокируется.
2. Вал подаёт крутящий момент на солнце.
3. Вращение солнца заставляет планеты обкатываться вместе с ним.
4. Водило становится ведомым, сообщая пониженную передачу.

Управляя элементами простой «планетарки», получают разные характеристики:

Передача	Как работает планетарная коробка в АКПП
1	Солнце подаёт вращение на водило, корона двигается в противоположную сторону.
2	Корона подаёт вращение на водило, солнце зафиксировано.
3	Ведущее водило передаёт вращение солнцу. Корона заблокирована.
4	Водило двигает корону. Солнце зафиксировано.
Задний ход	Водило заблокировано. Солнечное колесо вращается, планеты обкатывают и двигают корону в противоположную сторону.

Кпд η простой передачи достигает 0,97.

Планетарный ряд с одной степенью свободы становится планетарной передачей. Две степени образуют дифференциал. Дифференциал складывает моменты на ведомом колесе, поступающие от основных ведущих звеньев.

Разновидности планетарных передач

По количеству ступеней планетарные механизмы разделяют на:

• однорядные;
• многорядные.

Планетарная передача из одной солнечной шестерни, одновенцовых сателлитов, водила и эпицикла будет однорядной. Замена сателлитов на двухвенцовые усложняет конструкцию, делая её двухрядной.

Многоступенчатая планетарная коробка передач — это последовательно установленные однорядные блоки. Такая схема позволяет суммировать передаточные числа и получать большие значения. 4-скоростные АКПП состоят из двухрядных планетарных конструкций, 8-скоростные — из четырёхрядных.

В АКПП применяют схемы, названные в честь изобретателей:

• Механизм Уилсона представляет собой трёхрядную конструкцию, в которой соединены корона первого, водило второго и корона третьего рядов. Количество передач — 5 прямых и 1 задняя.
• Механизм Лепелетье состоит из 3 соосно расположенных простых планетарных передач. Количество передач — 6 прямых и 1 задняя.
• Схема Симпсона — 2 редуктора с общей солнечной шестернёй. Водило второго ряда оборудовано тормозом. Корона первого ряда и солнце через две блокировочные муфты жёстко соединены с ведущим валом. Механизм реализует режимы: нейтраль; 1,2,3 передачи; задний ход.

По типу зубчатых конструкций планетарные редукторы делятся на:

• цилиндрические;
• конические;
• волновые;
• червячные.

Разные типы применяют для передачи момента между валами, расположенными параллельно или под углом. А также в механизмах, требующих низкой или высокой кинематической характеристики.

Характеристики основных разновидностей этого устройства

В конструкции планетарного ряда АКПП применяют различные типы зубчатых передач. Выделяют три основные наиболее распространенные: цилиндрические, конические и волновые.

Цилиндрические

Зубчатые механизмы передают момент между параллельными валами. В конструкцию цилиндрической передачи входит две и более пар колёс. Форма зубьев шестерней может быть прямой, косой или шевронной. Цилиндрическая схема простая в производстве и действии. Применяется в коробках передач, бортовых редукторах, приводах. Передаточное число ограничено размерами механизма: для одной колёсной пары достигает 12. КПД — 95%.

Конические

Колёса в конической схеме преобразуют и передают вращение между валами, расположенными под углом от 90 до 170 градусов. Зубья нагружены неравномерно, что снижает их предельный момент и прочность. Присутствие сил на осях усложняет конструкцию опор. Для плавности соединения и большей выносливости применяют круговую форму зубьев.

Производство конических передач требует высокой точности, поэтому обходится дорого. Угловые конструкции применяются в редукторах, затворах, фрезерных станках. Передаточное отношение конических механизмов для техники средней грузоподъёмности не превышает 7. КПД — 98%.

Волновые

Во волновой передаче отсутствуют солнечная и планетные шестерни. Внутри коронного колеса установлено гибкое зубчатое колесо в форме овала. Водило выступает в качестве генератора волн, и выглядит в виде овального кулачка на специальном подшипнике.

Гибкое стальное или пластмассовое колесо под действием водила деформируется. По большой геометрической оси зубья сцепляются с короной на всю рабочую высоту, по малой оси зацепление отсутствует. Движение передаётся волной, создаваемой гибким зубчатым колесом.

Во волновых механизмах КПД растёт вместе с передаточным числом, превышающим 300. Волновая передача не работает в схемах с кинематической характеристикой ниже 20. Редуктор выдает 85% КПД, мультипликатор — 65%. Конструкция применяется в промышленных роботах, манипуляторах, авиационной и космической технике.

Достоинства и недостатки планетарных передач

Планетарная передача выигрывает у простых зубчатых механизмов аналогичной мощности компактным размером и массой меньшей в 2 — 3 раза. Используя нескольких планетных шестерней, достигается зацепление зубьев на 80%. Нагрузочная способность механизма повышается, а давление на каждый зубец уменьшается.

Кинематическая характеристика планетарного механизма доходит до 1000 с малым числом зубчатых колёс без применения многорядных конструкций. Помимо передачи планетарная схема способна работать как дифференциал.

За счёт соосности валов планетарного механизма, компоновать машины проще, чем с другими редукторами.

Применение планетарного ряда в АКПП снижает уровень шума в салоне автомобиля. Сбалансированная система имеет высокую вибропрочность за счет демпфирования колебаний. Соответственно снижается вибрация кузова.

Недостатки планетарного механизма:

• сложное производство и высокая точность сборки;
• в сателлиты устанавливают подшипники, которые выходят из строят быстрее, чем шестерня;
• при повышении передаточных отношений КПД падает, поэтому приходится усложнять конструкцию.

Передаточное число планетарных передач

Передаточным называют отношение частоты ведущего вала планетарной передачи к частоте ведомого. Визуально определить его значение не получится. Механизм приводится в движение разными способами, а значит передаточное число в каждом случае различно.

Для расчёта передаточного числа планетарного редуктора учитывают число зубьев и систему закрепления. Допустим, у солнечной шестерни 24 зуба, у сателлита — 12, у короны — 48. Водило закреплено. Ведущим становится солнце.

Сателлиты начнут вращаться со скоростью, передаваемой солнечной шестернёй. Передаточное отношение равно: -24/12 или -2. Результат означает, что планеты вращаются в противоположном направлении от солнца с угловой скоростью 2 оборота. Сателлиты обкатывают корону и заставляют её обернуться на 12/48 или ¼ оборота. Колёса с внутренним закреплением вращаются в одном направлении, поэтому число положительное.

Общее передаточное число равно отношению числа зубьев ведущего колеса к количеству зубьев ведомого: -24/48 или -1/2 оборота делает корона относительно солнца при зафиксированном водиле.

Если водило станет ведомым при ведущем солнце, то передаточное отношение: (1+48/24) или 3. Это самое большое число, какое способна предложить система. Самое маленькое отношение получается при фиксировании короны и подачи момента на водило: (1+/(1+48/24)) или 1/3.

Передаточные числа простой планетарной схемы: 1,25 — 8, многоступенчатой: 30 — 1000. С ростом кинематической характеристики КПД снижается.

Подбор чисел зубьев планетарных передач

Число зубьев колёс подбирают на первом этапе расчёта планетарной схемы по заранее установленному передаточному отношению. Особенность проектирования планетарного ряда заключается в соблюдении требований правильной сборки, соосности и соседства механизма:

• зубья сателлитов должны совпадать с впадинами солнца и эпицикла;
• планеты не должны задевать друг друга зубьями. На практике более 6 сателлитов не используют из-за трудностей равномерного распределения нагрузки;
• оси водила, солнечного и коронного колёс должны совпадать.

Основное соотношение подбора зубьев передачи через передаточное число выглядит так:

i = 1+Zкорона/Zсолнце,

где  i — передаточное число;

Zn — количество зубьев.

Условие соосности соблюдается при равных межосевых расстояниях солнечного колеса, короны и водила. Для простой планетарной зубчатой передачи проверяют межосевые расстояния между центральными колёсами и сателлитами. Равенство должно удовлетворять формуле:

Zкорона= Zсолнце+2×Zсателлит.

Чтобы между планетами оставался зазор, сумма радиусов соседних шестерней не должна превышать осевое расстояние между ними. Условие соседства с солнечным колесом проверяют по формуле:

sin (π/c)> (Zсателлит+2)/(Zсолнце+Zсателлит),

где с — количество сателлитов.

Планетные колёса размещаются равномерно, если соотношение зубьев короны и солнца к количеству сателлитов окажется целым:

Zсолнце/с = Z;

Zкорона/с = Z,

где Z — целое число.

Расчет на прочность планетарных передач

Прочностной расчёт планетарных передач проводят как для цилиндрических зубчатых передач. Вычисляют каждое зацепление:

• внешнее — между солнцем и планетными колёсами;
• внутреннее — между планетами и короной.

Если колёса изготовлены из одного материала, а силы в зацеплении равны, рассчитывают наименее прочное соединение — внешнее.

Алгоритм расчёта следующий:

1. Выбирают схему редуктора.
2. Определяют исходные данные: передаточное число i, крутящий момент Твых и частоту вращения выходного вала Uвых.
3. Подбирают число зубьев с проверкой условий сборки и соседства планетных шестерней.
4. Рассчитывают угловые скорости колёс.
5. Вычисляют КПД и моменты выходных валов.
6. Рассчитывают прочность зацепления.

В расчёте момента учитывают количество планетных колёс и неравномерное нагружение их зубьев. Вводят поправочный коэффициент η =1,5…2, если меры выравнивания отсутствуют:

• повышенная точность изготовления;
• радиальная подвижность солнца, короны или водила;
• применение упругих элементов.

Расчёт зубчатых передач выполняют по двум критериям:

• контактная прочность, т.е. выносливость рабочих поверхностей зубьев под нагрузкой;
• напряжение на изгиб, усталостный излом.

Расчёт контактной прочности сводится к проверке условия, что напряжение σн не превышает допустимого значения. Вычисления проводят по формуле Герца для цилиндрических поверхностей, добавляя уточняющие коэффициенты. В результате получают значение межосевого расстояния — главную геометрическую характеристику зубчатой передачи:

d=K×η×∛ (T×Kн(i±1))/(Ψ×i×[σн]^2),

где K — вспомогательный коэффициент для прямозубых колёс, МПа;

η — коэффициент неравномерности;

Т — вращающий момент, Н×мм;

Kн — коэффициент нагрузки;

Ψ — коэффициент ширины колеса равный 0,75;

i — передаточное число;

[σн] — допускаемое контактное напряжение, МПа. Определяется коэффициентом долговечности и пределом выносливости.

После определения геометрии передачи проверяют условие прочности:

σн= {310/(d×i)}×√ (T×Kн(i+1)^3)/(Ψ×d) ≤ [σн]

При расчёте на изгиб принимают условие, что вся нагрузка передаётся одной паре зубьев и приложена к его вершине. Расчётное напряжение не должно превышать допускаемое:

σf= (M/W) – (F/(b×s) ≤ [σf],

где М — изгибающий момент;

W — осевой момент сопротивления;

F — сила сжатия;

b, s — размеры зуба в сечении;

[σf] — допускаемое напряжение изгиба. Зависит от предела выносливости, шероховатости, погрешности изготовления зубьев.

Советы по подбору планетарного редуктора

Перед выбором планетарного редуктора проводят точный расчёт нагружения и режимов работы механизма. Определяют тип передачи, осевые нагрузки, температурный диапазон и типоразмеры редуктора. Для тяжёлой спецтехники, где нужен большой крутящий момент при малых скоростях, выбирают редуктор с высоким передаточным отношением.

Чтобы сбавить угловую скорость, не снижая крутящего момента, применяют привод с электродвигателем и редуктором. При выборе мотор редуктора учитывают:

• эксплуатационную нагрузку;
• момент вала на выходе;
• частоту вращения входного и выходного валов;
• мощность электродвигателя;
• монтажное исполнение.

Область применения планетарных передач

Планетарная схема используется в:

• редукторах;
• автоматических и механических коробках передач;
• в приводах летательных аппаратов;
• дифференциалах машин, приборов;
• ведущих мостах тяжёлой техники;
• кинематических схемах металлорежущих станков.

Планетарную коробку передач применяют в агрегатах с переменным передаточным отношением, затормаживая водило. В гусеничной технике для сложения потоков мощности элементы в планетарном механизме не блокируют.

Заключение

Планетарные передачи в АКПП зарекомендовали себя десятилетиями эксплуатации со времён Ford T: компактными размерами, малым весом, высокими скоростями, надёжностью и выносливостью. Планетарная схема способна передавать вращение и управлять потоками мощности, поэтому нашла применение в авиации, машиностроении, промышленности.

Чтобы не ошибиться с выбором конструкции, проводят точный расчёт геометрии и прочности зубчатой передачи, сверяя с допустимыми значениями. Ошибки вычислений приводят к чрезмерной нагрузке зубчатых передач, поломке и истиранию зубьев.

Зубчатое колесо — Википедия

Зубча́тое колесо́ или шестерня́^[1], зубчатка^[2] — основная деталь зубчатой передачи в виде диска с зубьями на цилиндрической или конической поверхности, входящими в зацепление с зубьями другого зубчатого колеса.

Обычно термины зубчатое колесо, шестерня, зубчатка являются синонимами, но некоторые авторы называют ведущее зубчатое колесо шестернёй, а ведомое — колесом^[2]. Происхождение слова «шестерня́» доподлинно неизвестно, хотя встречаются предположения о связи с числом «шесть». Л. В. Куркина, однако, выводит термин из слова «шест» (в смысле «ось»)^[3].

Зубчатые колёса обычно используются па́рами с разным числом зубьев с целью преобразования крутящего момента и числа оборотов валов на входе и выходе. Колесо, к которому крутящий момент подводится извне, называется ведущим, а колесо, с которого момент снимается — ведомым. Если диаметр ведущего колеса меньше, то крутящий момент ведомого колеса увеличивается за счёт пропорционального уменьшения скорости вращения, и наоборот. В соответствии с передаточным отношением, увеличение крутящего момента будет вызывать пропорциональное уменьшение угловой скорости вращения ведомой шестерни, а их произведение — механическая мощность — останется неизменным. Данное соотношение справедливо лишь для идеального случая, не учитывающего потери на трение и другие эффекты, характерные для реальных устройств.

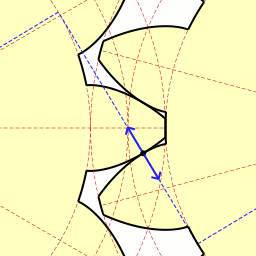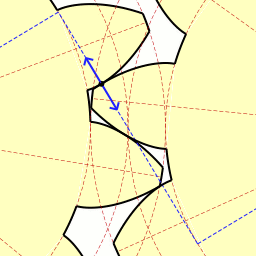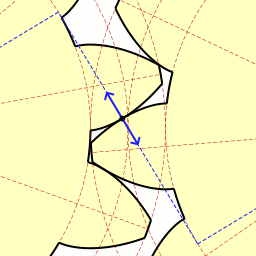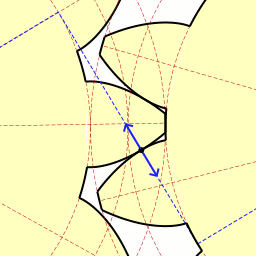Движение точки соприкосновения зубьев с эвольвентным профилем;
слева — ведущее, справа — ведомое колесо Параметры зубчатого колеса

Профиль зубьев колёс как правило имеет эвольвентную боковую форму. Однако существуют передачи с круговой формой профиля зубьев (передача Новикова с одной и двумя линиями зацепления) и с циклоидальной. Кроме того, в храповых механизмах применяются зубчатые колёса с несимметричным профилем зуба.

Параметры эвольвентного зубчатого колеса:

• m — модуль колеса. Модулем зацепления называется линейная величина в π раз меньшая окружного шага P или отношение шага по любой концентрической окружности зубчатого колеса к π, то есть модуль — число миллиметров диаметра делительной окружности приходящееся на один зуб. Тёмное и светлое колёсо имеют одинаковый модуль. Самый главный параметр, стандартизирован, определяется из прочностного расчёта зубчатых передач. Чем больше нагружена передача, тем выше значение модуля. Через него выражаются все остальные параметры. Модуль измеряется в миллиметрах, вычисляется по формуле:

m=dz=pπ{\displaystyle \mathbf {m={\frac {d}{z}}={\frac {p}{\pi }}} }

• z — число зубьев колеса
• p — шаг зубьев (отмечен сиреневым цветом)
• d — диаметр делительной окружности (отмечена жёлтым цветом)
• d_a — диаметр окружности вершин тёмного колеса (отмечена красным цветом)
• d_b — диаметр основной окружности — эвольвенты (отмечена зелёным цветом)
• d_f — диаметр окружности впадин тёмного колеса (отмечена синим цветом)
• h_aP+h_fP — высота зуба тёмного колеса, x+h_aP+h_fP — высота зуба светлого колеса

В машиностроении приняты определённые значение модуля зубчатого колеса m для удобства изготовления и замены зубчатых колёс, представляющие собой целые числа или числа с десятичной дробью: 0,5; 0,7; 1; 1,25; 1,5; 1,75; 2; 2,5; 3; 3,5; 4; 4,5; 5 и так далее до 50. (подробнее см. ГОСТ 9563-60 Колеса зубчатые. Модули)

Зубчатые колеса могут быть изготовлены с различным смещением режущей рейки: без смещения (нулевое зубчатое колесо или «с нулевыми зубцами»), с положительным смещением (смещение в сторону увеличения материала), с отрицательным смещением (смещение в сторону уменьшения материала).

Высота головки зуба — h_aP и высота ножки зуба — h_fP — в случае нулевого зубчатого колеса соотносятся с модулем m следующим образом: h_aP = m; h_fP = 1,25 m, то есть:

hfPhaP=1,25{\displaystyle \mathbf {{\frac {h_{fP}}{h_{aP}}}=1,25} }

Отсюда получаем, что высота зуба h (на рисунке не обозначена):

h=hfP+haP=2,25m{\displaystyle \mathbf {h={h_{fP}}+{h_{aP}}=2,25m} }

Вообще из рисунка ясно, что диаметр окружности вершин d_a больше диаметра окружности впадин d_f на двойную высоту зуба h. Исходя из всего этого, если требуется практически определить модуль m зубчатого колеса, не имея нужных данных для вычислений (кроме числа зубьев z), то необходимо точно измерить его наружный диаметр d_a и результат разделить на число зубьев z плюс 2:

m=daz+2{\displaystyle \mathbf {m={\frac {d_{a}}{z+2}}} }

Продольная линия зуба[править | править код]

Зубчатые колеса классифицируются в зависимости от формы продольной линии зуба на:

• прямозубые
• косозубые
• шевронные

Прямозубые колёса[править | править код]

Прямозубые колёса — самый распространённый вид зубчатых колёс. Зубья расположены в радиальных плоскостях, а линия контакта зубьев обеих шестерён параллельна оси вращения. При этом оси обеих шестерён также должны располагаться строго параллельно. Прямозубые колеса имеют наименьшую стоимость, но, в то же время, предельный крутящий момент таких колес ниже, чем косозубых и шевронных.

Косозубые колёса[править | править код]

Косозубые колёса являются усовершенствованным вариантом прямозубых. Их зубья располагаются под углом к оси вращения, а по форме образуют часть винтовой линии.

• Достоинства:
  • Зацепление таких колёс происходит плавнее, чем у прямозубых, и с меньшим шумом.
  • Площадь контакта увеличена по сравнению с прямозубой передачей, таким образом, предельный крутящий момент, передаваемый зубчатой парой, тоже больше.
• Недостатками косозубых колёс можно считать следующие факторы:
  • При работе косозубого колеса возникает механическая сила, направленная вдоль оси, что вызывает необходимость применения для установки вала упорных подшипников;
  • Увеличение площади трения зубьев (что вызывает дополнительные потери мощности на нагрев), которое компенсируется применением специальных смазок.

В целом, косозубые колёса применяются в механизмах, требующих передачи большого крутящего момента на высоких скоростях, либо имеющих жёсткие ограничения по шумности.

Шевронные колеса[править | править код]

Изобретение шевронной передачи часто приписывают Андре Ситроену, однако на самом деле он лишь выкупил патент на более совершенную схему, которую придумал польский механик-самоучка^[4]. Зубья таких колёс изготавливаются в виде буквы «V» (либо они получаются стыковкой двух косозубых колёс со встречным расположением зубьев). Передачи, основанные на таких зубчатых колёсах, обычно называют «шевронными».

Шевронные колёса решают проблему осевой силы. Осевые силы обеих половин такого колеса взаимно компенсируются, поэтому отпадает необходимость в установке валов на упорные подшипники. При этом передача является самоустанавливающейся в осевом направлении, по причине чего в редукторах с шевронными колесами один из валов устанавливают на плавающих опорах (как правило — на подшипниках с короткими цилиндрическими роликами).

Зубчатые колёса с внутренним зацеплением[править | править код]

При жёстких ограничениях на габариты, в планетарных механизмах, в шестерённых насосах с внутренним зацеплением, в приводе башни танка, применяют колёса с зубчатым венцом, нарезанным с внутренней стороны. Вращение ведущего и ведомого колеса совершается в одну сторону. В такой передаче меньше потери на трение, то есть выше КПД.

Секторные колёса[править | править код]

Секторное колесо представляет собой часть обычного колеса любого типа. Такие колёса применяются в тех случаях, когда не требуется вращение звена на полный оборот, и поэтому можно сэкономить на его габаритах.

Колёса с круговыми зубьями[править | править код]

Передача на основе колёс с круговыми зубьями (Передача Новикова) имеет ещё более высокие ходовые качества, чем косозубые — высокую нагрузочную способность зацепления, высокую плавность и бесшумность работы. Однако они ограничены в применении сниженными, при тех же условиях, КПД и ресурсом работы, такие колёса заметно сложнее в производстве. Линия зубьев у них представляет собой окружность радиуса, подбираемого под определённые требования. Контакт поверхностей зубьев происходит в одной точке на линии зацепления, расположенной параллельно осям колёс.

Конические колёса в приводе затвора плотины Главная передача в заднеприводном автомобиле

Во многих машинах осуществление требуемых движений механизма связано с необходимостью передать вращение с одного вала на другой при условии, что оси этих валов пересекаются. В таких случаях применяют коническую зубчатую передачу. Различают виды конических колёс, отличающихся по форме линий зубьев: с прямыми, тангенциальными, круговыми и криволинейными зубьями. Конические колёса с круговым зубом, например, применяются в автомобильных главных передачах коробки передач.

Реечная передача (кремальера) применяется в тех случаях, когда необходимо преобразовать вращательное движение в поступательное и обратно. Состоит из обычной прямозубой шестерни и зубчатой планки (рейки). Работа такого механизма показана на рисунке.

Зубчатая рейка представляет собой часть колеса с бесконечным радиусом делительной окружности. Поэтому делительная окружность, а также окружности вершин и впадин превращаются в параллельные прямые линии. Эвольвентный профиль рейки также принимает прямолинейное очертание. Такое свойство эвольвенты оказалось наиболее ценным при изготовлении зубчатых колёс.

Также реечная передача применяется в зубчатой железной дороге.

Цевочная передача Коронная шестерня

Коронное колесо — особый вид колёс, зубья которых располагаются на боковой поверхности. Такое колесо, как правило, стыкуется с обычным прямозубым, либо с барабаном из стержней (цевочное колесо), как в башенных часах. Передачи с цевочным колесом — одни из самых ранних и просты в изготовлении, но характеризуются очень большими потерями на трение.

Зубчатые барабаны киноаппаратуры — предназначены для точного перемещения киноплёнки за перфорацию. В отличие от обычных зубчатых колес, входящих в зацепление с другими колесами или зубчатыми профилями, зубчатые барабаны киноаппаратуры имеют шаг зубьев, выбранный в соответствии с шагом перфорации. Большинство таких барабанов имеет эвольвентный профиль зубьев, изготавливаемых по тем же технологиям, что и в остальных зубчатых колесах.

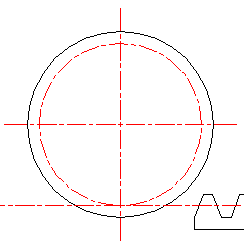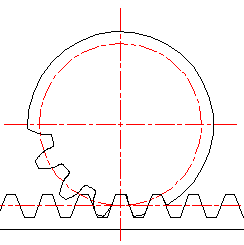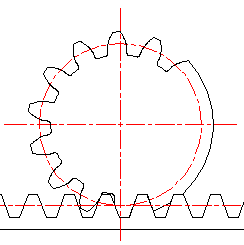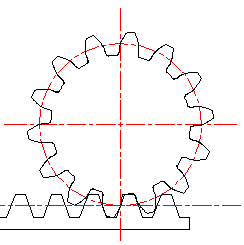
Метод обката[править | править код]

В настоящее время является наиболее технологичным, а поэтому и самым распространённым способом изготовления зубчатых колёс. При изготовлении зубчатых колёс могут применяться такие инструменты, как гребёнка, червячная фреза и долбяк.

Метод обката с применением гребёнки[править | править код]

Нарезание зубчатого колеса на зубофрезерном станке с помощью червячной фрезы Червячная фреза

Режущий инструмент, имеющий форму зубчатой рейки, называется зуборезной гребёнкой. На одной стороне гребёнки по контуру её зубьев затачивается режущая кромка. Заготовка накатываемого колеса совершает вращательное движение вокруг оси. Гребёнка совершает сложные перемещения, состоящие из поступательного движения перпендикулярно оси колеса и возвратно-поступательного движения (на анимации не показано), параллельного оси колеса для снятия стружки по всей ширине его обода. Относительное движение гребёнки и заготовки может быть и иным, например, заготовка может совершать прерывистое сложное движение обката, согласованное с движением резания гребёнки. Заготовка и инструмент движутся на станке друг относительно друга так, как будто происходит зацепление профиля нарезаемых зубьев с исходным производящим контуром гребёнки.

Метод обката с применением червячной фрезы[править | править код]

Помимо гребёнки в качестве режущего инструмента применяют червячную фрезу. В этом случае между заготовкой и фрезой происходит червячное зацепление.

Метод обката с применением долбяка[править | править код]

Зубчатые колёса также долбят на зубодолбёжных станках с применением специальных долбяков. Зубодолбёжный долбяк представляет собой зубчатое колесо, снабжённое режущими кромками. Поскольку срезать сразу весь слой металла обычно невозможно, обработка производится в несколько этапов. При обработке инструмент совершает возвратно-поступательное движение относительно заготовки. После каждого двойного хода, заготовка и инструмент поворачиваются относительно своих осей на один шаг. Таким образом, инструмент и заготовка как бы «обкатываются» друг по другу. После того, как заготовка сделает полный оборот, долбяк совершает движение подачи к заготовке. Этот процесс происходит до тех пор, пока не будет удалён весь необходимый слой металла.

Метод копирования (Метод деления)[править | править код]

Дисковой или пальцевой фрезой нарезается одна впадина зубчатого колеса. Режущая кромка инструмента имеет форму этой впадины. После нарезания одной впадины заготовка поворачивается на один угловой шаг при помощи делительного устройства, операция резания повторяется.

Метод применялся в начале XX века. Недостаток метода состоит в низкой точности: впадины изготовленного таким методом колеса сильно отличаются друг от друга.

Горячее и холодное накатывание[править | править код]

Процесс основан на последовательной деформации нагретого до пластического состояния слоя определённой глубины заготовки зубонакатным инструментом. При этом сочетаются индукционный нагрев поверхностного слоя заготовки на определённую глубину, пластическая деформация нагретого слоя заготовки для образования зубьев и обкатка образованных зубьев для получения заданной формы и точности.

Изготовление конических колёс[править | править код]

Деревянная форма для изготовления зубчатого колеса из музея Geararium, 1896 год

Технология изготовления конических колёс теснейшим образом связана с геометрией боковых поверхностей и профилей зубьев. Способ копирования фасонного профиля инструмента для образования профиля на коническом колесе не может быть использован, так как размеры впадины конического колеса изменяются по мере приближения к вершине конуса. В связи с этим такие инструменты, как модульная дисковая фреза, пальцевая фреза, фасонный шлифовальный круг, можно использовать только для черновой прорезки впадин или для образования впадин колёс не выше восьмой степени точности.

Для нарезания более точных конических колёс используют способ обкатки в станочном зацеплении нарезаемой заготовки с воображаемым производящим колесом. Боковые поверхности производящего колеса образуются за счёт движения режущих кромок инструмента в процессе главного движения резания, обеспечивающего срезание припуска. Преимущественное распространение получили инструменты с прямолинейным лезвием. При прямолинейном главном движении прямолинейное лезвие образует плоскую производящую поверхность. Такая поверхность не может образовать эвольвентную коническую поверхность со сферическими эвольвентными профилями. Получаемые сопряжённые конические поверхности, отличающиеся от эвольвентных поверхностей, называют квазиэвольвентными.

Моделирование[править | править код]

Ошибки при проектировании зубчатых колёс[править | править код]

Зуб, подрезанный у основания

Подрезание зуба[править | править код]

Согласно свойствам эвольвентного зацепления, прямолинейная часть исходного производящего контура зубчатой рейки и эвольвентная часть профиля зуба нарезаемого колеса касаются только на линии станочного зацепления. За пределами этой линии исходный производящий контур пересекает эвольвентный профиль зуба колеса, что приводит к подрезанию зуба у основания, а впадина между зубьями нарезаемого колеса получается более широкой. Подрезание уменьшает эвольвентную часть профиля зуба (что приводит к сокращению продолжительности зацепления каждой пары зубьев проектируемой передачи) и ослабляет зуб в его опасном сечении. Поэтому подрезание недопустимо. Чтобы подрезания не происходило, на конструкцию колеса накладываются геометрические ограничения, из которых определяется минимальное число зубьев, при котором они не будут подрезаны. Для стандартного инструмента это число равняется 17. Также подрезания можно избежать, применив способ изготовления зубчатых колёс, отличный от способа обкатки. Однако и в этом случае условия минимального числа зубьев нужно обязательно соблюдать, иначе впадины между зубьями меньшего колеса получатся столь тесными, что зубьям большего колеса изготовленной передачи будет недостаточно места для их движения и передача заклинится.

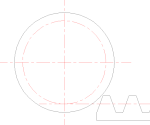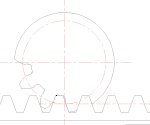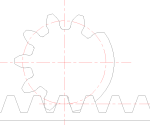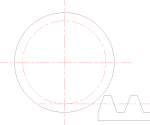Подрезание зуба 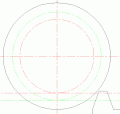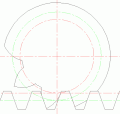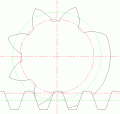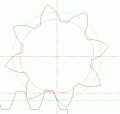Заострение зуба

Для уменьшения габаритных размеров зубчатых передач колёса следует проектировать с малым числом зубьев. Поэтому при числе зубьев меньше 17, чтобы не происходило подрезания, колёса должны быть изготовлены со смещением инструмента — увеличением расстояния между инструментом и заготовкой (корригированные зубчатые колеса).

Заострение зуба[править | править код]

При увеличении смещения инструмента толщина зуба будет уменьшаться. Это приводит к заострению зубьев. Опасность заострения особенно велика у колёс с малым числом зубьев (менее 17). Для предотвращения скалывания вершины заострённого зуба смещение инструмента ограничивают сверху.

Зубчатые передачи используются у личинок насекомых рода Issus для синхронизации движения ног в момент прыжка.^[5][6]

Зубчатое колесо и шестерёнка являются искусственными негеральдическими фигурами, которые получили очень широкое распространение в международной, территориальной и родовой геральдике. Эта эмблема появилась в эпоху машинного производства во второй половине XIX — начале XX века. Чаще всего зубчатое колесо олицетворяет промышленность, технический и научный прогресс, индустриализацию, модернизацию^[7]. В послевоенные годы шестерню в СССР широко использовали в муниципальной геральдике Советского Союза.

Изображения зубчатых колёс присутствуют на многих гербах и эмблемах, в числе которых: