Как правильно пользоваться динамометрическим ключом? Использование, применение и затягивание динамометрическим ключом
Сегодня динамометрический ключ является одним из самых распространенных приспособлений в сфере ремонта различной техники. Для чего предназначен динамометрический ключ? Инструмент нужен для того, чтобы передать на крепеж необходимое усилие, которое обеспечивает надежную фиксацию скрепляемых деталей. Несмотря на то, что это приспособление применяется уже около 100 лет в различных сферах деятельности, где встречаются резьбовые соединения, у некоторых возникает вопрос, как же правильно пользоваться динамометрическим ключом.
Инструкция по эксплуатации и применению динамометрического ключа
Чтобы передать на резьбовое соединение необходимое усилие, нужно правильно использовать любой динамометрический ключ. При применении инструмента необходимо соблюдать основные рекомендации и правила пользования динамометрическим ключом:
- Использование ключа в качестве обычного воротка или трещотки увеличит износ инструмента, поэтому ключ нужно применять только по назначению;
- Для обеспечения точности передаваемого усилия рекомендуется использовать только один переход сборного инструмента, т.
 е одну торцевую головку между затягиваемым крепежом и присоединительным квадратом ключа;
е одну торцевую головку между затягиваемым крепежом и присоединительным квадратом ключа; - Запрещается увеличение плеча рычага с помощью разнообразных удлинителей, например, трубы;
- Не рекомендуется бросать или стучать по инструменту;
- Если ключ был только купленили давно не использовался, то для того чтобы внутренние механизмы инструмента смазались, необходимо сделать несколько нагружений на минимальном значении диапазона крутящего момента;
- После работы ключ лучше хранить в чистом и сухом месте. А при долгом хранении лучше произвести процедуру консервации, смазав корпус ключа тонким слоем масла;
- После измерений инструмент необходимо выставлять на начальное нулевое значение, чтобы пружина механизма не растягивалась, сохраняя точность измерений инструмента;
- Впоследствии пружина в ключах все равно ослабевает. Поэтому ежегодно или чаще необходимо производить проверку и регулировку (калибровку/поверку) инструмента на специальном стенде, чтобы повысить точность инструмента.

Ознакомившись с основными инструкциями по применению динамометрических ключей, предлагаем разобраться, как правильно затягивать болты динамометрическим ключом разных видов этого инструмента. В предыдущей статье мы рассматривали основные виды динамометрических ключей, их особенности, преимущества и недостатки.
Как пользоваться динамометрическим ключом щелчкового типа?
Данный вид ключей является самым распространенным и популярным инструментом среди профессионалов и любителей. Во время работы не нужно контролировать значения усилия. Принцип работы динамометрического ключа заключается в следующем: при достижении заранее выставленного значения силы, ключ издаст щелчок, который означает о завершении работы и инструмент, проскальзывая, не будет передавать на крепеж большее усилие, чем было установлено на шкалах инструмента.
Для того, чтобы правильно пользоваться динамометрическим ключом щелчкового типа необходимо знать, как выставляется нужное значение с помощью основной и вспомогательной шкалы.
Руководство по эксплуатации динамометрического ключа щелчкового типа:
- Раскрутить стопорную гайку внизу рукоятки ключа;
- Выставить значение нагрузки на основной вертикальной шкале с помощью вращающейся рукояти. И если необходимо, то нужно выставить значение крутящего момента на дополнительной круговой шкале внизу ручки, чтобы получить требуемое значение силы. Получается, что значение складываются с обеих шкал, фиксируя итоговое усилие;
- Закручиваем стопорную гайку внизу рукоятки ключа, чтобы зафиксировать выставленное усилие;
Теперь Вы знаете, как выставить момент затяжки на динамометрическом ключе. В зависимости от варианта ключа, шкалы могут иметь определенные отличия, например, различные цены делений, вид исполнения шкал или обозначение усилия в различных системах измерений (Н/м, Кг/м или в Футофунты lbf/ft). В каталоге AIST представлены различные щелчковые предельные ключи.
Закручивать резьбовое соединение необходимо до характерного звука ключа, который оповещает о достижении выставленного усилия. При щелчке сработает специальный фиксатор механизма ключа, который не даст передать на крепеж большее усилие, чем был выставлено на инструменте. После окончания работ необходимо выставить ключ на минимальное значение диапазона крутящего момента и закрутить фиксатор ключа.
При щелчке сработает специальный фиксатор механизма ключа, который не даст передать на крепеж большее усилие, чем был выставлено на инструменте. После окончания работ необходимо выставить ключ на минимальное значение диапазона крутящего момента и закрутить фиксатор ключа.
Предлагаем посмотреть видео инструкцию: “Как пользоваться щелчковым динамометрическим ключом”
Подобные модели динамометрических ключей для автомобиля являются самыми востребованными на рынке. Имея небольшую стоимость инструмент удобен в работе, обеспечивает необходимую точность и прост в использовании.
Динамометрический ключ стрелочный: как пользоваться правильно?
В отличие от предыдущего вида инструмента, стрелочный ключ не имеет возможности выставить усилие заранее. Начало контролируемого диапазона динамометрических ключей от 0 Нм, поэтому значение прилагаемого усилия необходимо контролировать во время работы, что может показаться не очень удобным, особенно в труднодоступных местах. При этом точность измерений оставляет желать лучшего, так как можно приложить к крепежу большее усилие, поэтому при работе необходимо соблюдать крайнюю осторожность.
Начало контролируемого диапазона динамометрических ключей от 0 Нм, поэтому значение прилагаемого усилия необходимо контролировать во время работы, что может показаться не очень удобным, особенно в труднодоступных местах. При этом точность измерений оставляет желать лучшего, так как можно приложить к крепежу большее усилие, поэтому при работе необходимо соблюдать крайнюю осторожность.
Как работает динамометрический ключ данного вида? Принцип действия довольно прост. Во время работы на определенный угол смещается рукоятка со шкалой значений, а указатель остается неподвижным.
Перед тем как пользоваться динамометрическим ключом подобного исполнения, необходимо изучить значения измерений шкалы и определить то положение указателя, при котором необходимо закончить работу. Шкала ключа может иметь различные значения измерений усилия. Это могут быть не только привычные Н/м, но и Кг/м или в Футофунты (lbf/ft), поэтому перед затяжкой необходимо точно определить, на каком значении шкалы необходимо закончить прикладывать усилие.
- 1 Кг/м ~ 10 Н/м;
- 1 Кг/м ~ 7,2 lbf/ft (Футофунты).
Как пользоваться динамометрическим ключом со стрелкой:
- Точно определить необходимое значение на шкале;
- Плавно, без резких движений производить затягивание резьбового соединения, контролируя показания указателя по шкале;
- Закончить работу при достижении необходимого усилия.
После просмотра видео станет понятно, как правильно пользоваться стрелочным динамометрическим ключом.
Первые два варианта инструмента относятся к шкальным динамометрическим ключам. В первом случае усилие устанавливается с помощью шкал, а во втором — контролируется по шкале.
Как затягивать цифровым динамометрическим ключом?
Подобный вид инструмента похож на предельный ключ, только вместо пружинного механизма, цифровой ключ использует электронную “начинку”, благодаря которой измеряется усилие. Принцип работы электронного динамометрического ключа: необходимое значение выставляется также заранее, а при его достижении ключ издает звуковой сигнал, оповещающий о завершении работы. На цифровом дисплее можно контролировать изменения прилагаемого усилия в конкретную точку времени.
Принцип работы электронного динамометрического ключа: необходимое значение выставляется также заранее, а при его достижении ключ издает звуковой сигнал, оповещающий о завершении работы. На цифровом дисплее можно контролировать изменения прилагаемого усилия в конкретную точку времени.
Вся номенклатура данного инструмента является измерительными приборами, поэтому ключи требуют бережного хранения и должны использоваться строго по назначению.
Перед приобретением инструмента рекомендуем ознакомиться с материалом — Рекомендации по выбору динамометрических ключей
Ключи динамометрические в категории «Инструмент»
Ключ динамометрический моментный TOPTUL 3/8″х385mm 19-110Nm ANAF1211 ТОП
На складе в г. Харьков
Доставка по Украине
2 823 грн
Купить
Харьков
Ключ динамометрический электронный TOPTUL 4. 2-85Нм (двустороннего действия) 3/8″ укороченный DT-085S3 ТОП
2-85Нм (двустороннего действия) 3/8″ укороченный DT-085S3 ТОП
На складе в г. Харьков
Доставка по Украине
10 722 грн
Купить
Харьков
Динамометрический ключ с индикацией TOPTUL 20-200Нм (цифровой) 1/2″ DT-200N0 ТОП
На складе в г. Харьков
Доставка по Украине
11 092 грн
Купить
Харьков
Динамометрический ключ 1/2″ TOPTUL 500mm 40-200Nm ANAM1620 ТОП
На складе в г. Харьков
Доставка по Украине
4 340 грн
Купить
Харьков
Динамометрический ключ с индикацией TOPTUL 10-100Нм (цифровой) 3/8″ DT-100N ТОП
На складе в г. Харьков
Доставка по Украине
10 370 грн
Купить
Харьков
Мощный динамометрический ключ 1/2″ 28-210NM INTERTOOL XT-9006 ROM
На складе
Доставка по Украине
1 430. 40 грн
40 грн
1 788 грн
Купить
Мощный динамометрический ключ 3/8″ 7-105NM INTERTOOL XT-9003 ROM
На складе
Доставка по Украине
1 335.20 грн
1 669 грн
Купить
Мощный динамометрический ключ 1/4″ 2-24NM INTERTOOL XT-9001 ROM
На складе
Доставка по Украине
1 529.60 грн
1 912 грн
Купить
Динамометрический ключ 1/2″ переходник 1/2 х 3/8 удлинитель 125 мм 1/2 28-210 NM INTERTOOL XT-9007
На складе в г. Киев
Доставка по Украине
1 039.20 грн
1 299 грн
Купить
Ключ динамометрический TOPTUL 3/4″x1000mm 100-800Nm ANAS2480 ТОП
На складе в г. Харьков
Доставка по Украине
18 213 грн
Купить
Харьков
Динамометрический ключ 3/8″ 7-105 NM INTERTOOL XT-9003
На складе в г. Киев
Доставка по Украине
857. 22 грн
22 грн
1 099 грн
Купить
Динамометрический ключ стрелочный Top Tools 37D105
На складе
Доставка по Украине
525 грн
590 грн
Купить
Динамометрический ключ INTERTOOL XT-9003 3/8″, 7-105 Нм
На складе в г. Запорожье
Доставка по Украине
813 грн
1 099 грн
Купить
Запорожье
Динамометрический ключ 1/2″ переходник 1/2 х 3/8, удлинитель 125 мм 1/2 28-210 NM INTERTOOL XT-9007
На складе в г. Харьков
Доставка по Украине
969 — 999 грн
от 2 продавцов
999 грн
1 299 грн
Купить
Харьков
Динамометрический ключ 1/4″, 2-24 NM INTERTOOL XT-9001
На складе в г. Киев
Доставка по Украине
1 039.20 грн
1 299 грн
Купить
Смотрите также
Jonnesway T04250 Динамометрический ключ, 70-350 Нм
На складе в г.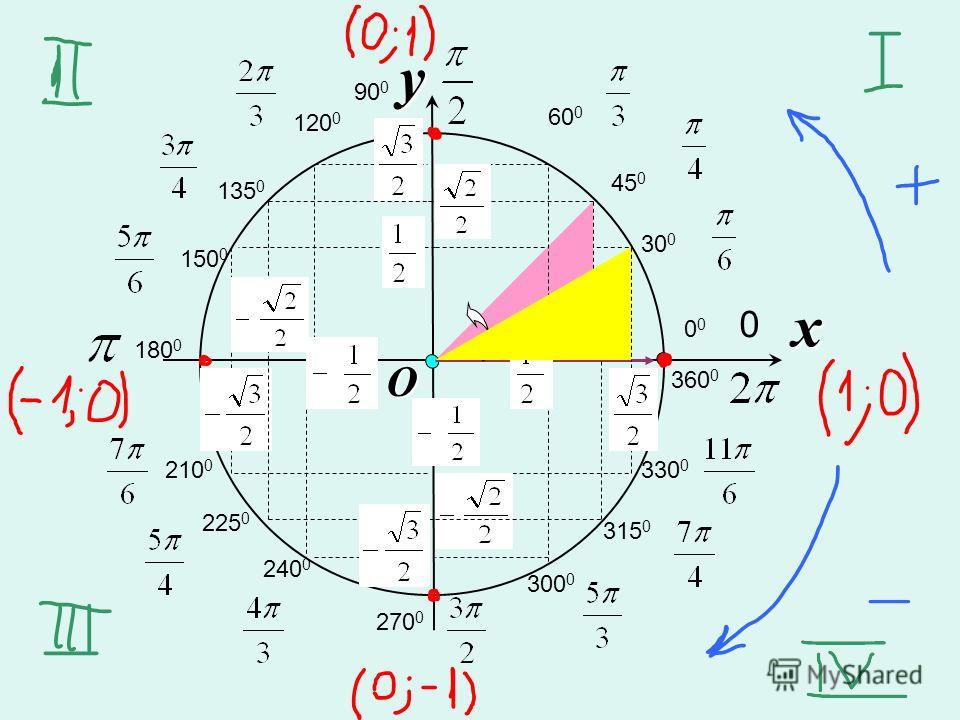 Киев
Киев
Доставка по Украине
4 405.67 грн
Купить
Динамометрический ключ MTX 42-210 Нм/ 1/2″ (141609)
На складе в г. Киев
Доставка по Украине
1 687.82 грн
Купить
Jonnesway T04061 Динамометрический ключ, 10-60 Нм,3/8″
На складе в г. Киев
Доставка по Украине
2 108.83 грн
Купить
Jonnesway T04300 Динамометрический ключ, 3/4″, 400 Нм
На складе в г. Киев
Доставка по Украине
от 6 985.35 грн
Купить
Динамометрический ключ Jonnesway 140-700 Нм (T04500)
На складе в г. Киев
Доставка по Украине
16 050.50 грн
Купить
Динамометрический ключ 1/2″ TOPTUL 535mm 40-210Nm ANAF1621 ТОП
На складе в г. Харьков
Доставка по Украине
3 429 грн
Купить
Харьков
Динамометрический ключ JBM 1/4″ 2-24NM 270мм. (51262)
(51262)
На складе в г. Нововолынск
Доставка по Украине
2 197.05 грн
2 265 грн
Купить
Нововолынск
Динамометрический ключ для колес 17/19/21 1/2 28-210 Нм Mar-Pol
На складе
Доставка по Украине
995 грн
1 300 грн
Купить
Динамометрический ключ INTERTOOL XT-9003
На складе в г. Запорожье
Доставка по Украине
809 — 816 грн
от 2 продавцов
809 грн
1 099 грн
Купить
Запорожье
Ключ динамометрический Dnipro-M 1/4″ 5-25 Нм
Заканчивается
Доставка по Украине
1 316.70 грн
1 386 грн
Купить
Ключ динамометрический Dnipro-M 1/2″ 40-220 Нм
Заканчивается
Доставка по Украине
1 993.10 грн
2 098 грн
Купить
Ключ динамометрический Dnipro-M 1/2″ 20-120 Нм
Заканчивается
Доставка по Украине
1 709. 1 — 1 894.3 грн
1 — 1 894.3 грн
от 2 продавцов
1 894.30 грн
1 994 грн
Купить
Ключ динамометрический 3/8″ 19-110NM Profline 39003
На складе
Доставка по Украине
по 875 грн
от 2 продавцов
875 грн
Купить
Ключ динамометрический 1/2 28-210 Нм Falcon F07002
На складе в г. Сумы
Доставка по Украине
по 899 грн
от 2 продавцов
899 грн
Купить
Тригонометрия
Тригонометрия (от греческого trigonon «треугольник» + метрон «мера»)
Хотите изучить тригонометрию? Вот краткий обзор.
Перейдите по ссылкам, чтобы узнать больше, или перейдите к Указатель тригонометрии
| Тригонометрия … это все о треугольниках. |
Тригонометрия помогает нам находить углы и расстояния и широко используется в науке, технике, видеоиграх и многом другом!
Прямоугольный треугольник
Наиболее интересным треугольником является прямоугольный треугольник.
Другой угол часто обозначается θ, и тогда называются три стороны:
- Смежный : смежный (рядом) угол θ
- Напротив : напротив угла θ
- и самая длинная сторона Гипотенуза
Почему треугольник прямоугольный?
Почему этот треугольник так важен?
Представьте, что мы можем измерять вдоль и поперек, но хотим знать прямое расстояние и угол:
Тригонометрия может найти недостающий угол и расстояние.
Или, может быть, у нас есть расстояние и угол, и нам нужно «начертить точку» вдоль и поперек:
Подобные вопросы часто встречаются в инженерии, компьютерной анимации и т. д.
И тригонометрия дает ответы!
Синус, косинус и тангенс
Основными функциями в тригонометрии являются синус, косинус и тангенс

Для любого угла « θ «:
(Синус, косинус и тангенс часто обозначаются как sin, cos и tan.)
Пример: чему равен синус 35°?
Используя этот треугольник (длина только до одного десятичного знака):
sin(35°) = Противоположный Гипотенуза = 2,8 4,9 = 0,57…
Треугольник может быть больше, меньше или повернут, но этот угол всегда будет иметь отношение .
Калькуляторы имеют sin, cos и tan, чтобы помочь нам, поэтому давайте посмотрим, как их использовать:
Пример. Какой высоты дерево?
Мы не можем добраться до верхушки дерева, поэтому отходим и измеряем угол (с помощью транспортира) и расстояние (с помощью лазера):
- Мы знаем Гипотенузу
- И мы хотим знать Противоположный
Синус есть отношение Противоположность/Гипотенуза :
sin(45°) = Напротив Гипотенуза
Получите калькулятор, введите «45», затем клавишу «sin»:
sin(45°) = 0,7071. ..
..
Что означает 0,7071… значит? Это отношение длин сторон, поэтому противоположная сторона в раз длиннее гипотенузы примерно в 0,7071 раз.
Теперь мы можем положить 0,7071 … вместо греха (45 °):
0,7071 … = напротив Гипотенериз
, а мы также знаем, что гипотенуз — 20 5
, а мы также знаем, что гипотенуз — 20 5559 9
, а мы также знаем, что гипотенуз — 20 59
и мы также знаем, что гипотенуза :
0,7071… = Напротив 20
Чтобы решить, сначала умножьте обе части на 20:
20 × 0,7071… = Противоположный
Наконец:
Противоположный = 14,14 м (до 2 знаков после запятой)
Когда вы наберете больше опыта, вы можете сделать это быстро следующим образом:Пример: Какова высота дерева?
Начать с:sin(45°) = Напротив Гипотенуза
Мы знаем: 0,7071. .. = Напротив 20
.. = Напротив 20
Поменять стороны: Напротив 20 = 0,7071…
Умножить обе стороны на 20 : Противоположная = 0,7071… × 20
Вычислить: Противоположная = 14,14
(до 2 знаков после запятой)
1 4
Высота дерева
Попробуйте Sin Cos и Tan
Поиграйте с этим некоторое время (переместите мышь) и познакомьтесь со значениями синуса, косинуса и тангенса для различных углов, таких как 0°, 30°, 45°, 60° и 90°.
../алгебра/изображения/круг-треугольник.js
Также попробуйте 120°, 135°, 180°, 240°, 270° и т. д. и обратите внимание, что позиций может быть положительный или отрицательный по правилам декартовых координат, поэтому синус, косинус и тангенс также меняются между положительным и отрицательным.
Итак, тригонометрия тоже касается кругов !
Единичный круг
То, с чем вы только что играли, это Единичный круг.
Это круг радиусом 1 с центром в точке 0.
Поскольку радиус равен 1, мы можем напрямую измерить синус, косинус и тангенс.
Здесь мы видим синусоидальную функцию единичного круга:
изображения/circle-sine.js
Примечание: вы можете увидеть красивые графики, сделанные с помощью синуса, косинуса и тангенса.
градусов и радианов
Углы могут быть в градусах или радианах. Вот несколько примеров:
| Уголок | градусов | радиан |
|---|---|---|
| Прямоугольный | 90° | №/2 |
| __ Прямоугольный | 180° | № |
| Полный оборот | 360° | 2π |
Повторяющийся шаблон
Поскольку угол вращается вокруг и вокруг круга , функции синуса, косинуса и тангенса повторяются один раз за каждый полный оборот (см. Амплитуда, период, фазовый сдвиг и частота).
Амплитуда, период, фазовый сдвиг и частота).
Когда мы хотим вычислить функцию для угла, превышающего полный оборот в 360° (2π радиан), мы вычитаем столько полных оборотов, сколько необходимо, чтобы вернуть угол ниже 360° (2π радиан):
Пример: чему равен косинус 370°?
370° больше 360°, поэтому вычтем 360°
370° − 360° = 10°
cos(370°) = cos(10°) = 0,985 (до 3 знаков после запятой)
А когда угол меньше нуля, просто добавить полные обороты.
Пример: чему равен синус −3 радиан?
−3 меньше 0, поэтому добавим 2π радиан
−3 + 2π = −3 + 6,283… = 3,283… радиан
sin(−3) = sin(3,283…) = −0,141 (до 3 знаков после запятой)
Решение треугольников
Тригонометрия также полезна для общих треугольников, а не только прямоугольных.
Помогает нам в решении треугольников. «Решение» означает нахождение недостающих сторон и углов.
Пример: найти недостающий угол «C»
Угол C можно найти, прибавив углы треугольника к 180°:
Итак, C = 180° − 76° − 34° = 70°
Мы также можем найти недостающие длины сторон. Общее правило:
Общее правило:
Когда мы знаем любые 3 стороны или угла, мы можем найти остальные 3
(кроме случая с тремя углами)
Подробнее см. раздел «Решение треугольников».
Другие функции (котангенс, секанс, косеканс)
Подобно синусу, косинусу и тангенсу, существуют три другие тригонометрические функции , которые получаются путем деления одной стороны на другую:
Функция косеканса: | csc( θ ) = гипотенуза / напротив |
Секущая Функция: | сек( θ ) = гипотенуза / соседняя |
Котангенс Функция: | детская кроватка( θ ) = Смежный/Напротив |
Тригонометрические и треугольные тождества
И по мере того, как вы будете лучше разбираться в тригонометрии, вы сможете выучить следующее:
Тригонометрические тождества — это уравнения, которые верны для всех прямоугольных треугольников . | |
Тождества треугольников — это уравнения, которые верны для всех треугольников (они не обязательно должны иметь прямой угол). |
Станьте экспертом по треугольникам (и кругам)!
| На последних страницах вы видели довольно много тригонометрических тождеств. Удобно иметь их сводку для справки. Эти тождества в основном относятся к одному углу, обозначенному θ , но есть и такие, которые включают два угла, и для них два угла обозначаются α и β . | |
Более важные тождества.Вам не нужно знать все личности навскидку. Но это вы должны. | |
Определяющие отношения для тангенса, котангенса, секанса и косеканса через синус и косинус. | |
| Формула Пифагора для синусов и косинусов. Это, вероятно, самая важная триггерная идентичность. | |
| Тождества, выражающие триггерные функции через их дополнения. В этом нет ничего особенного. Каждая из шести триггерных функций равна своей кофункции, оцениваемой под дополнительным углом. | |
| Периодичность триггерных функций. Синус, косинус, секанс и косеканс имеют период 2 π , а тангенс и котангенс имеют период π . | |
| Тождества для отрицательных углов. Синус, тангенс, котангенс и косеканс — нечетные функции, а косинус и секанс — четные функции. | |
| Тождества Птолемея, формулы суммы и разности для синуса и косинуса. | |
Формулы двойного угла для синуса и косинуса. Обратите внимание, что существует три формы формулы двойного угла для косинуса. Вам нужно знать только одно, но уметь вывести два других из формулы Пифагора. Вам нужно знать только одно, но уметь вывести два других из формулы Пифагора. | |
Менее важные тождества.Вы должны знать, что эти личности есть, но они не так важны, как упомянутые выше. Все они могут быть получены из приведенных выше, но иногда для этого требуется некоторая работа. | |
| Формула Пифагора для тангенсов и секансов. Есть также один для котангенсов и косекансов, но, поскольку котангенсы и косекансы нужны редко, он не нужен. | |
| Тождества, выражающие триггерные функции через их дополнения. | |
| Формулы суммы, разности и двойного угла для тангенса. | |
Формулы половинного угла. Синус и косинус принимают положительный или отрицательный квадратный корень в зависимости от квадранта угла θ /2. Например, если θ /2 — острый угол, то будет использоваться положительный корень. | |
Совершенно неясные личности.Они просто здесь для извращенности. Нет, не совсем. У них есть несколько приложений, но обычно это узкие приложения, и о них можно просто забыть, пока они не понадобятся. | |
| Тождества произведения-суммы. Эта группа тождеств позволяет преобразовать сумму или разность синусов или косинусов в произведение синусов и косинусов. | |
Идентификаторы продуктов. В стороне: как ни странно, эти тождества произведений использовались до того, как были изобретены логарифмы для выполнения умножения. Вот как можно использовать второй. Если вы хотите умножить x умножить на y, используйте таблицу, чтобы найти угол α , косинус которого равен x , и угол β , косинус которого равен y . Найдите косинусы суммы α + β . а разница α – β .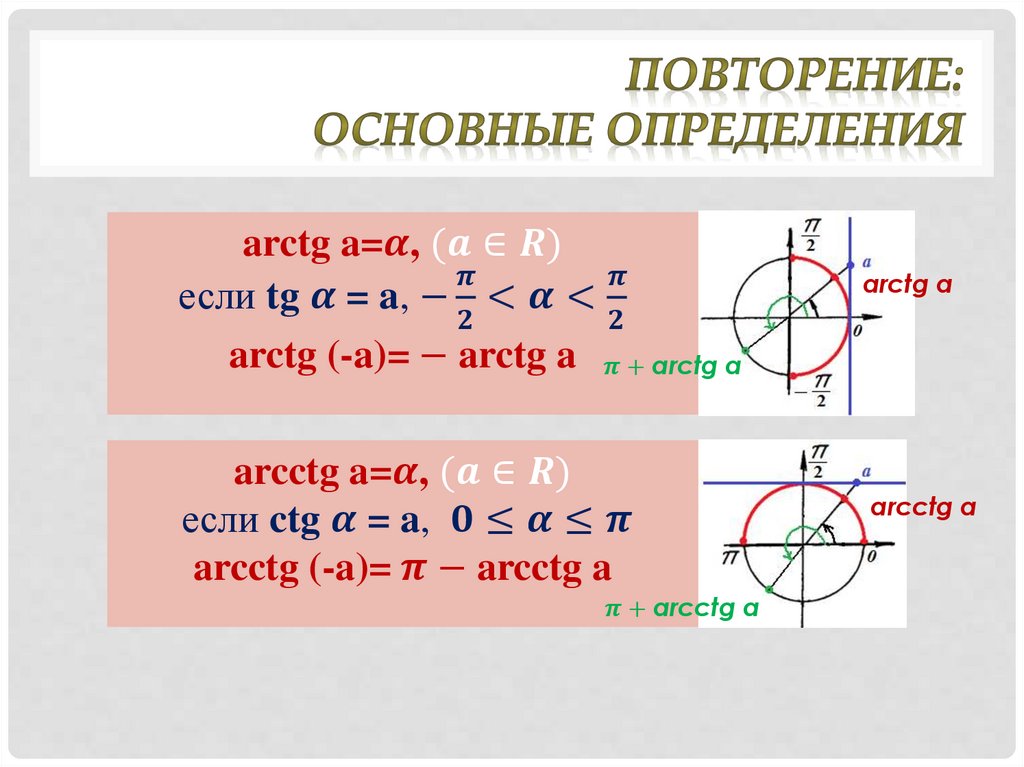 | |

 е одну торцевую головку между затягиваемым крепежом и присоединительным квадратом ключа;
е одну торцевую головку между затягиваемым крепежом и присоединительным квадратом ключа;
