Как правильно пользоваться динамометрическим ключом? Использование, применение и затягивание динамометрическим ключом
Сегодня динамометрический ключ является одним из самых распространенных приспособлений в сфере ремонта различной техники. Для чего предназначен динамометрический ключ? Инструмент нужен для того, чтобы передать на крепеж необходимое усилие, которое обеспечивает надежную фиксацию скрепляемых деталей. Несмотря на то, что это приспособление применяется уже около 100 лет в различных сферах деятельности, где встречаются резьбовые соединения, у некоторых возникает вопрос, как же правильно пользоваться динамометрическим ключом.
Инструкция по эксплуатации и применению динамометрического ключа
Чтобы передать на резьбовое соединение необходимое усилие, нужно правильно использовать любой динамометрический ключ. При применении инструмента необходимо соблюдать основные рекомендации и правила пользования динамометрическим ключом:
- Использование ключа в качестве обычного воротка или трещотки увеличит износ инструмента, поэтому ключ нужно применять только по назначению;
- Для обеспечения точности передаваемого усилия рекомендуется использовать только один переход сборного инструмента, т.
е одну торцевую головку между затягиваемым крепежом и присоединительным квадратом ключа; - Запрещается увеличение плеча рычага с помощью разнообразных удлинителей, например, трубы;
- Не рекомендуется бросать или стучать по инструменту;
- Если ключ был только купленили давно не использовался, то для того чтобы внутренние механизмы инструмента смазались, необходимо сделать несколько нагружений на минимальном значении диапазона крутящего момента;
- После работы ключ лучше хранить в чистом и сухом месте. А при долгом хранении лучше произвести процедуру консервации, смазав корпус ключа тонким слоем масла;
- После измерений инструмент необходимо выставлять на начальное нулевое значение, чтобы пружина механизма не растягивалась, сохраняя точность измерений инструмента;
- Впоследствии пружина в ключах все равно ослабевает. Поэтому ежегодно или чаще необходимо производить проверку и регулировку (калибровку/поверку) инструмента на специальном стенде, чтобы повысить точность инструмента.
е одну торцевую головку между затягиваемым крепежом и присоединительным квадратом ключа;
Ознакомившись с основными инструкциями по применению динамометрических ключей, предлагаем разобраться, как правильно затягивать болты динамометрическим ключом разных видов этого инструмента. В предыдущей статье мы рассматривали основные виды динамометрических ключей, их особенности, преимущества и недостатки.
Как пользоваться динамометрическим ключом щелчкового типа?
Данный вид ключей является самым распространенным и популярным инструментом среди профессионалов и любителей. Во время работы не нужно контролировать значения усилия. Принцип работы динамометрического ключа заключается в следующем: при достижении заранее выставленного значения силы, ключ издаст щелчок, который означает о завершении работы и инструмент, проскальзывая, не будет передавать на крепеж большее усилие, чем было установлено на шкалах инструмента.
Для того, чтобы правильно пользоваться динамометрическим ключом щелчкового типа необходимо знать, как выставляется нужное значение с помощью основной и вспомогательной шкалы.
Руководство по эксплуатации динамометрического ключа щелчкового типа:
- Раскрутить стопорную гайку внизу рукоятки ключа;
- Выставить значение нагрузки на основной вертикальной шкале с помощью вращающейся рукояти. И если необходимо, то нужно выставить значение крутящего момента на дополнительной круговой шкале внизу ручки, чтобы получить требуемое значение силы. Получается, что значение складываются с обеих шкал, фиксируя итоговое усилие;
- Закручиваем стопорную гайку внизу рукоятки ключа, чтобы зафиксировать выставленное усилие;
Теперь Вы знаете, как выставить момент затяжки на динамометрическом ключе. В зависимости от варианта ключа, шкалы могут иметь определенные отличия, например, различные цены делений, вид исполнения шкал или обозначение усилия в различных системах измерений (Н/м, Кг/м или в Футофунты lbf/ft). В каталоге AIST представлены различные щелчковые предельные ключи.
Закручивать резьбовое соединение необходимо до характерного звука ключа, который оповещает о достижении выставленного усилия.
При щелчке сработает специальный фиксатор механизма ключа, который не даст передать на крепеж большее усилие, чем был выставлено на инструменте. После окончания работ необходимо выставить ключ на минимальное значение диапазона крутящего момента и закрутить фиксатор ключа.
Предлагаем посмотреть видео инструкцию: “Как пользоваться щелчковым динамометрическим ключом”
Подобные модели динамометрических ключей для автомобиля являются самыми востребованными на рынке. Имея небольшую стоимость инструмент удобен в работе, обеспечивает необходимую точность и прост в использовании.
Динамометрический ключ стрелочный: как пользоваться правильно?
В отличие от предыдущего вида инструмента, стрелочный ключ не имеет возможности выставить усилие заранее.
Как работает динамометрический ключ данного вида? Принцип действия довольно прост. Во время работы на определенный угол смещается рукоятка со шкалой значений, а указатель остается неподвижным.
Перед тем как пользоваться динамометрическим ключом подобного исполнения, необходимо изучить значения измерений шкалы и определить то положение указателя, при котором необходимо закончить работу. Шкала ключа может иметь различные значения измерений усилия. Это могут быть не только привычные Н/м, но и Кг/м или в Футофунты (lbf/ft), поэтому перед затяжкой необходимо точно определить, на каком значении шкалы необходимо закончить прикладывать усилие.
- 1 Кг/м ~ 10 Н/м;
- 1 Кг/м ~ 7,2 lbf/ft (Футофунты).
Как пользоваться динамометрическим ключом со стрелкой:
- Точно определить необходимое значение на шкале;
- Плавно, без резких движений производить затягивание резьбового соединения, контролируя показания указателя по шкале;
- Закончить работу при достижении необходимого усилия.
После просмотра видео станет понятно, как правильно пользоваться стрелочным динамометрическим ключом.
Первые два варианта инструмента относятся к шкальным динамометрическим ключам. В первом случае усилие устанавливается с помощью шкал, а во втором — контролируется по шкале.
Как затягивать цифровым динамометрическим ключом?
Подобный вид инструмента похож на предельный ключ, только вместо пружинного механизма, цифровой ключ использует электронную “начинку”, благодаря которой измеряется усилие.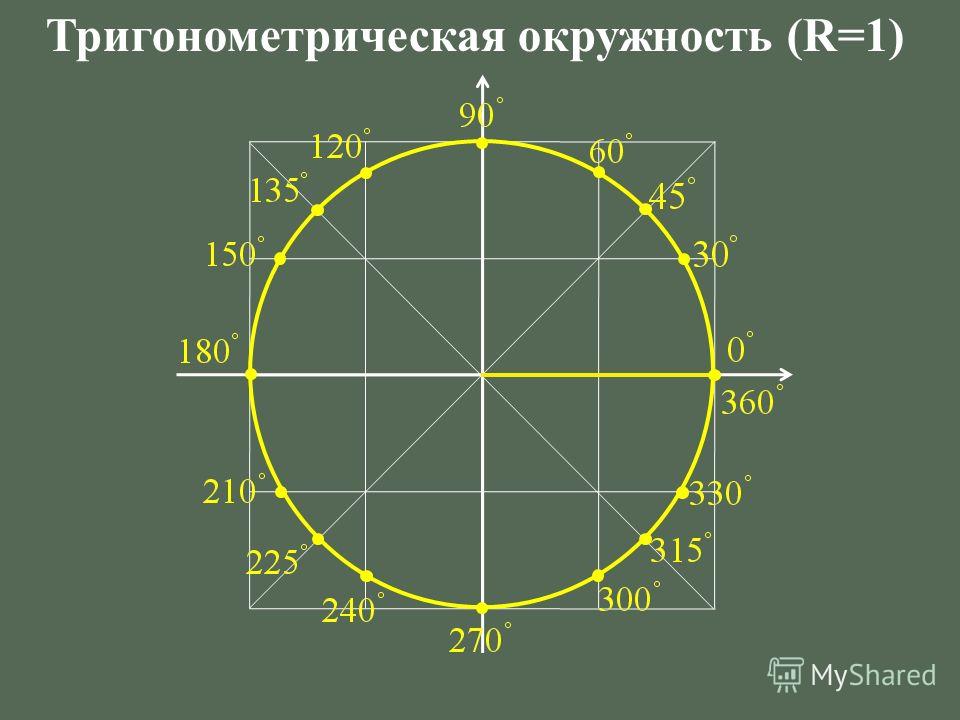
Принцип работы электронного динамометрического ключа: необходимое значение выставляется также заранее, а при его достижении ключ издает звуковой сигнал, оповещающий о завершении работы. На цифровом дисплее можно контролировать изменения прилагаемого усилия в конкретную точку времени.
Вся номенклатура данного инструмента является измерительными приборами, поэтому ключи требуют бережного хранения и должны использоваться строго по назначению.
Перед приобретением инструмента рекомендуем ознакомиться с материалом — Рекомендации по выбору динамометрических ключей
ЭБ СПбПУ — Исследование криптостойкости тригонометрического шифра с помощью эволюционных алгоритмов: выпускная …
|
Разрешенные действия: – Действие ‘Прочитать’ будет доступно, если вы выполните вход в систему или будете работать с сайтом на компьютере в другой сети Действие ‘Загрузить’ будет доступно, если вы выполните вход в систему или будете работать с сайтом на компьютере в другой сети Группа: Анонимные пользователи Сеть: Интернет |
03.03 — Прикладная информатика ; 09.03.03_03 — Прикладная информатика в области информационных ресурсов
03.03
Аннотация
Данная работа относится к сфере информационной безопасности и защите информации.
В первой главе приводится анализ предметной области: описывается современное положение криптоанализа, приводятся основные типы шифров. Также в первой главе раскрывается положение эволюционных алгоритмов в современном криптоанализе; приводится основной принцип алгоритма пчелиной колонии. Во второй главе теоретически описывается тригонометрический шифр и производится анализ его пространства поиска ключей. Далее теоретически описывается алгоритм пчелиной колоний, и, основываясь на предыдущих выводах, формируется принцип реализации алгоритма для криптоанализа тригонометрического шифра. В третьей главе приводится программная реализация штатного шифратора/дешифатора тригонометрического шифра, а также алгоритма пчелиной колонии для криптоанализа данного шифра. В четвертой главе производится сравнение результатов алгоритма криптоанализа с уже существующим генетическим алгоритмом для криптоанализа тригонометрического шифра, на основе полученных данных формируются выводы о криптостойкости шифра, а также проводится сравнительный анализ двух подходов к криптоанализу.
This work relates to the field of information security and information security. The first chapter provides an analysis of the subject area: describes the current situation of cryptanalysis, presents the main types of ciphers. Also in the first chapter the position of evolutionary algorithms in modern cryptanalysis is revealed, then, the basic principle of the bee colony algorithm is given. The second chapter theoretically describes the trigonometric cipher and analyzes its key search space. Next, the bee colony algorithm is theoretically described, and, based on previous findings, the principle of the algorithm implementation for cryptanalysis of a trigonometric cipher is formed. The third chapter provides a software implementation of the staff encoder / decoder of the trigonometric cipher, as well as the bee colony algorithm for cryptanalysis of this cipher. The fourth chapter compares the results of the cryptanalysis algorithm with the already existing genetic algorithm for cryptanalysis of the trigonometric cipher, based on the data obtained, conclusions are made about the cryptographic strength of the cipher, and a comparative analysis of two approaches to cryptanalysis is carried out.
Права на использование объекта хранения
| Место доступа | Группа пользователей | Действие | ||||
|---|---|---|---|---|---|---|
| Локальная сеть ИБК СПбПУ | Все | |||||
| Внешние организации №2 | Все | |||||
| Внешние организации №1 | Все | |||||
| Интернет | Авторизованные пользователи СПбПУ | |||||
| Интернет | Авторизованные пользователи (не СПбПУ, №2) | |||||
| Интернет | Авторизованные пользователи (не СПбПУ, №1) | |||||
| Интернет | Анонимные пользователи |
Статистика использования
На последних страницах вы видели довольно много тригонометрических тождеств. Удобно иметь их сводку для справки. Эти тождества в основном относятся к одному углу, обозначенному θ , но есть и такие, которые включают два угла, и для них два угла обозначаются α и β . | |
Более важные тождества.Вам не нужно знать все личности навскидку. Но это вы должны. | |
| Определяющие отношения для тангенса, котангенса, секанса и косеканса через синус и косинус. | |
| Формула Пифагора для синусов и косинусов. Это, вероятно, самая важная триггерная идентичность. | |
| Тождества, выражающие триггерные функции через их дополнения. В этом нет ничего особенного. Каждая из шести триггерных функций равна своей кофункции, оцениваемой под дополнительным углом. | |
Периодичность триггерных функций. Синус, косинус, секанс и косеканс имеют период 2 π , а тангенс и котангенс имеют период π . | |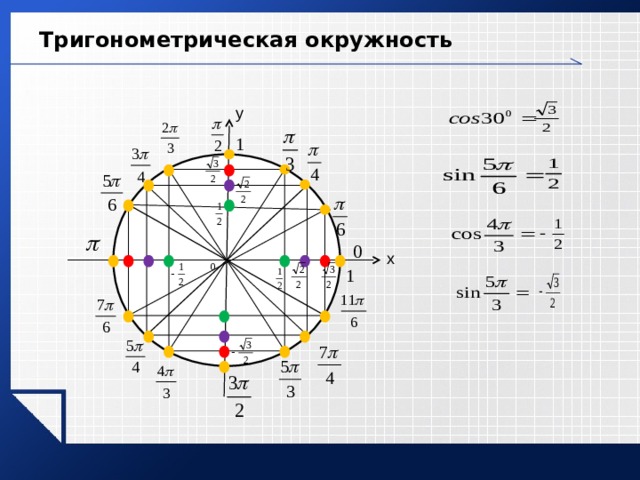
| Тождества для отрицательных углов. Синус, тангенс, котангенс и косеканс — нечетные функции, а косинус и секанс — четные функции. | |
| Тождества Птолемея, формулы суммы и разности для синуса и косинуса. | |
| Формулы двойного угла для синуса и косинуса. Обратите внимание, что существует три формы формулы двойного угла для косинуса. Вам нужно знать только одно, но уметь вывести два других из формулы Пифагора. | |
Менее важные тождества.Вы должны знать, что эти личности есть, но они не так важны, как упомянутые выше. Все они могут быть получены из приведенных выше, но иногда для этого требуется некоторая работа. | |
Формула Пифагора для тангенсов и секансов. Есть также один для котангенсов и косекансов, но, поскольку котангенсы и косекансы нужны редко, он не нужен. | |
| Тождества, выражающие триггерные функции через их дополнения. | |
| Формулы суммы, разности и двойного угла для тангенса. | |
| Формулы половинного угла. Синус и косинус принимают положительный или отрицательный квадратный корень в зависимости от квадранта угла θ /2. Например, если θ /2 — острый угол, то будет использоваться положительный корень. | |
Совершенно неясные личности.Они просто здесь для извращенности. Нет, не совсем. У них есть несколько приложений, но обычно это узкие приложения, и о них можно просто забыть, пока они не понадобятся. | |
| Тождества произведения-суммы. Эта группа тождеств позволяет преобразовать сумму или разность синусов или косинусов в произведение синусов и косинусов. | |
Идентификаторы продуктов.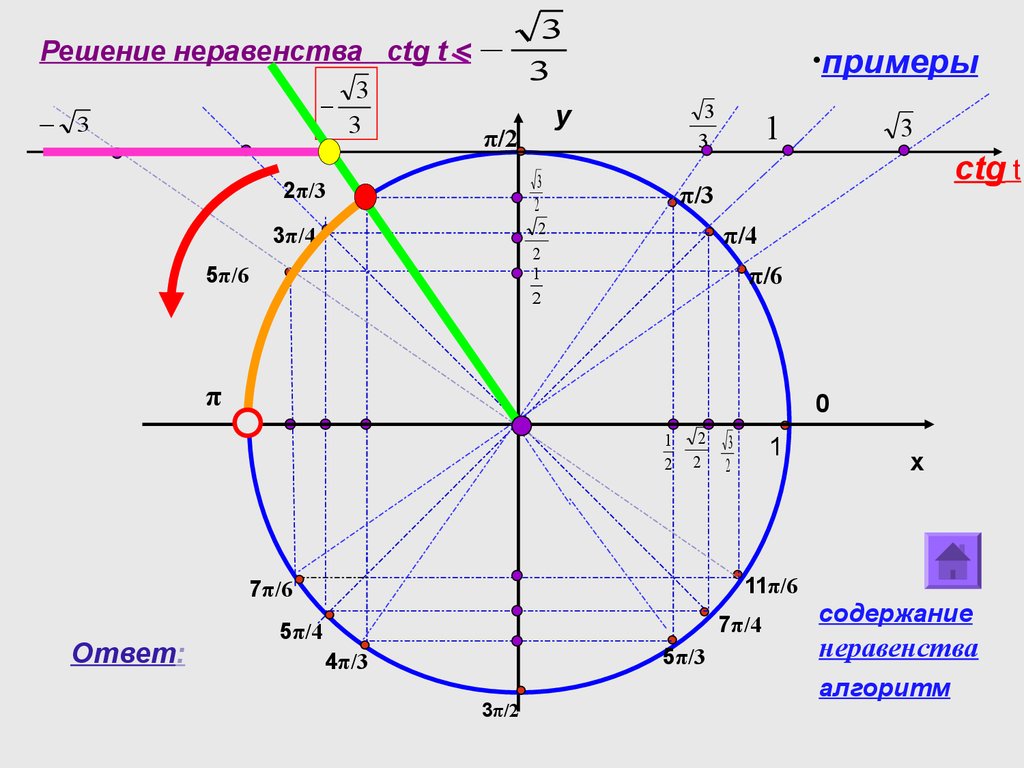 В стороне: как ни странно, эти тождества произведений использовались до того, как были изобретены логарифмы для выполнения умножения. Вот как можно использовать второй. Если вы хотите умножить x умножить на y, используйте таблицу, чтобы найти угол α , косинус которого равен x , и угол β , косинус которого равен y . Найдите косинусы суммы α + β . а разница α – β . Усредните эти два косинуса. Вы получаете товар xy ! Три поиска в таблице и вычисление суммы, разности и среднего, а не одного умножения. Тихо Браге (1546–1601), среди прочих, использовал этот алгоритм, известный как простафаэрез. | |
| Формулы тройного угла. Вы можете легко восстановить их по формулам сложения и двойного угла. | |
Больше формул половинного угла. Они описывают основные триггерные функции в терминах тангенса половины угла. Они используются в исчислении для особого вида замены в интегралах, иногда называемых Вейерштрассом t -замена. | |
13.2. Клавиши тригонометрических функций — Графический калькулятор от Mathlab: Руководство пользователя
Режимы RAD и DEG
Если тригонометрические функции выражены в градусах, коснитесь RAD, чтобы переключить калькулятор на DEG (режим градусов) . Все функции будут интерпретироваться в градусах.
Чтобы использовать тригонометрические функции в радианах, коснитесь DEG, чтобы вернуться к RAD (режим в радианах) . Функции будут интерпретироваться в радианах. Чтобы использовать градусы, добавьте символ градуса после аргументов.
Клавиша синуса
Клавиша синуса вычисляет значение синуса заданного угла, выраженное по умолчанию в радианах. Нажмите клавишу º (градусы) , чтобы ввести аргумент в градусах.
Пример
Вычисление sin45º – sin 2π/3
Расчетное решение
Примечание.
Не забудьте заключить в скобки значение радиана 2π/3.
Введите выражение и включите градусы: sin45º – sin (2π/3)
Клавиша арксинуса
Дважды нажмите клавишу синуса, чтобы использовать арксинус . Он используется для нахождения меры угла по значению его синуса.
Пример
Если sin A = 0,707, каково значение A?
Решение с помощью калькулятора
Чтобы найти A, возьмите арксинус 0,707. Дважды нажмите клавишу sine , затем введите 0,707.
Клавиша косеканса
Коснитесь клавиши синуса три раза, чтобы использовать косеканс функция.
Пример
Упрощение: CSC 45º — CSC 2π/3
Калькулятор. три раза.
Клавиша косинуса
Клавиша косинуса по умолчанию вычисляет косинус заданного угла, выраженного в радианах.
Чтобы использовать градусы, коснитесь º (градус) ключ после аргумента.
Пример
Вычисление: cos45º – cos 2π/3
Расчетное решение Клавиша арккосинуса Пример Расчет решения Клавиша секущей Пример Калькулятор Раствор Клавиша тангенса Пример Расчетное решение Клавиша арктангенса Пример Решение с помощью калькулятора Ключ котангенса
Введите выражение и включите градусы: cos45º – 9022/3π 20 (cos)
Дважды нажмите клавишу косинуса, чтобы использовать арккосинус . Он используется для нахождения меры угла по его косинусу.
Если cos A = 0,707, каково значение A?
Чтобы найти A, возьмите арккосинус 0,707. Дважды нажмите клавишу косинус , затем введите 0,707.
Нажмите клавишу синуса три раза, чтобы использовать секанс .
Упрощение: SEC 45º — SEC 2π/3
Введите выражение и включает в себя DEG: SEC 45º — (2π/3).
0290 cos три раза.
Клавиша тангенса по умолчанию вычисляет тангенс заданного угла в радианах. Нажмите клавишу º (градусы) , чтобы использовать градусы.
тангенс 45º – тангенс 2π/3
Введите выражение и включите градусы: тангенс 45º – 3 тангенс (20π
Дважды коснитесь клавиши тангенса, чтобы использовать арктангенс . Он используется для нахождения меры угла по значению его тангенса.
Если тангенс А = 0,707, каково значение А?
Чтобы решить, найдите арктангенс 0,707. Дважды коснитесь клавиши – загара , затем введите 0,707.
Нажмите кнопку tan три раза, чтобы найти котангенс .